Differenzierbarkeit


  • Lässt sich immer ein Zahlenwert für die lokale Änderungsrate finden?
  • Oder graphisch: kann man an jeden beliebigen Graphen in jedem Punkt eine Tangente anlegen?
  • Wie muss ein Graph beschaffen sein, dass das nicht möglich ist?



Die Betragsfunktion
`f(x) = |x|` nennt sich Betragsfunktion.
Sie ordnet jeder reellen Zahl ihren Betrag (also den Abstand zum Ursprung) zu.
Beispiele:
`f(+5) = 5`
`f(+2011) = 2011`
`f(-2011) = 2011`
`f(0) = 0`



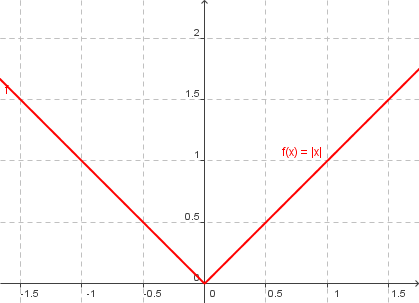
Graph der Betragsfunktion

Lokale Änderungsrate im Nullpunkt?
Bei `x_0 = 0`
  • gibt es keine eindeutige Tangente
  • ist `lim_(h->0) (f(x_0+h)-f(x_0))/h = +1` für positives h
  • ist `lim_(h->0) (f(x_0+h)-f(x_0))/h = -1` für negatives h
Bei so einem "Knick" lässt sich die lokale Änderungsrate nicht bestimmen.


Differenzierbarkeit
Eine Funktion f(x) heißt an einer Stelle `x_0` differenzierbar, wenn
`lim_(h->0) (f(x_0+h)-f(x_0))/h` so existiert,
dass sich für positives und negatives h der gleiche Wert ergibt.