Definition: Mittlere Änderungsrate
Mittlere Änderungsrate:
`hat f` = `(f(x_2)-f(x_1))/(x_2-x_1)`
`hat f` = `(f(x_2)-f(x_1))/(x_2-x_1)`
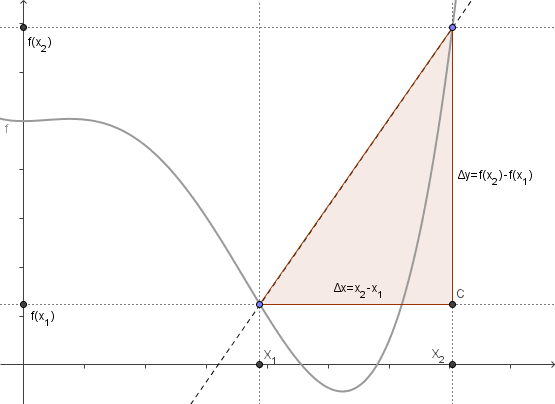
Graphische Darstellung der mittleren Änderungsrate
| UHU-Startseite►Mathematik►Jahrgangsstufen►11►Lokales Differenzieren►der Differenzenquotient und seine Deutung als Sekantensteigung bzw. mittlere Änderungsrate► |
|
Definition: Mittlere Änderungsrate Mittlere Änderungsrate: `hat f` = `(f(x_2)-f(x_1))/(x_2-x_1)`  Graphische Darstellung der mittleren Änderungsrate
|