|
Momentangeschwindigkeit: graphische Interpretation
| Zur Idee der Momentangeschwindigkeit |
Wie schnell bewegt sich ein fallender Körper (bei Vernachlässigung von Luftreibung) nach 1,0s?
- vorher: `bar v` für ein Zeitintervall (Durchschnittsgeschwindigkeit)
- jetzt: `v^text(*)` für einen bestimmten Zeitpunkt (Momentangeschwindigkeit)
- `v_1^text(*) = (f(1)-f(1))/(1-1) = 0/0` die bisherige Definition versagt!
- Existiert also gar keine Momentangeschwindigkeit?
| `bar v` |
Steigung der Geraden durch zwei Punkte des Graphen |
| `v^text(*)` |
Steigung von ... ? |
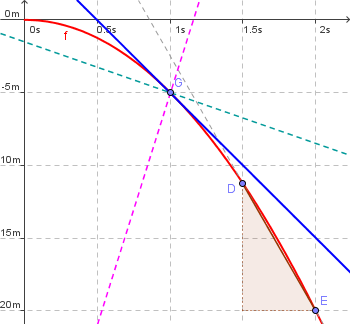
Sekante durch zwei Punkte; Geraden durch einen Punkt
- Von allen dargestellten Geraden durch G scheint die blaue den Funktionsverlauf am besten wiederzugeben
- weil ihre Steigung dort der Steigung des Graphen entspricht
- man nennt sie deshalb Tangente an den Graph von f im Punkt G
| Zur graphischen Bestimmung der Momentangeschwindigkeit |
- die Momentangeschwindigkeit lässt sich als Steigung der Tangente im Punkt G ablesen
- und hat in unserem Beispiel ungefähr den Wert -10 m/s
- Nachteil: graphische Bestimmung ist niemals exakt
|
