Durschnittsgeschwindigkeit
| Die Zeit-Höhen-Kurve beim freien Fall |
- vereinfachtes mathematisches Modell
- `f(x) = -5 x^2`
- x: Zeit in Sekunden
- y: Höhe in Metern
- zur Vereinfachung der Darstellung wird 9,81 auf 10 gerundet
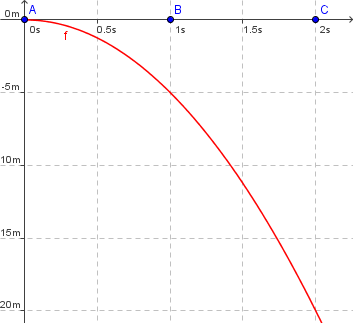
Vereinfachte Funktion für den freien Fall
| Durchschnittsgeschwindigkeit in der ersten und zweiten Sekunde |
- berechnet sich allgemein zu `bar v_(12) = (f(x_2)-f(x_1))/(x_2-x_1)`
- in der ersten Sekunde:
`bar v_(AB) = (f(1)-f(0))/(1-0) = (-5*1^2 - (-5*0^2))/(1 - 0) = -5/1`
Geschwindigkeit: -5 m/s
- in der zweiten Sekunde:
`bar v_(BC) = (f(2)-f(1))/(2-1) = (-5*2^2 - (-5*1^2))/(2 - 1) = -15/1`
Geschwindigkeit -15 m/s
- in der ersten und zweiten Sekunde:
`bar v_(AC) = (f(2)-f(0))/(2-0) = (-5*2^2 - (-5*0^2))/(2 - 0) = -20/2`
Geschwindigkeit: -10m/s

Darstellung verschiedener Durchschnittsgeschwindigkeiten
| Grafische Interpretation von `bar v` |
`bar v` entspricht Steigung der Strecke zwischen den zwei Punkten auf dem Graph.
`bar v_(12) = (Delta y)/(Delta x) = (f(x_2)-f(x_1))/(x_2-x_1)`
`bar v_(12) = (Delta y)/(Delta x) = (f(x_2)-f(x_1))/(x_2-x_1)`
| Aufgaben |
- Bestimmen Sie die Durchschnittsgeschwindigkeit für die ersten 5 Sekunden.
- Bestimmen Sie die Durchschnittsgeschwindigkeit in der 5 Fallsekunde.
- Ein Zug beschleunigt gleichmäßig so, dass sich für seine Wegfunktion `f(x) = 1/2*x^2` ergibt (x in Sekunden; f(x) in Metern). Bestimme die Durchschnittsgeschwindigkeit für die erste, zweite und dritte Sekunde.