UHU-Startseite►Mathematik►Jahrgangsstufen►12►Geraden und Ebenen im Raum►G9►Verwendung von Determinanten►2x2-Determinanten und ihre Entstehung►
Lösen eines inhomogenen 2x2-Systems


Ausgangsbasis
Gegeben ist das (2,2)-System:
`a_(11)x_1 + a_(21)x_2 = b_1`
`a_(12)x_1 + a_(22)x_2 = b_2`
mit folgenden Determinanten:
`D:=|(a_(11),a_(21)),(a_(12),a_(22))|; D_1:=|(b_1,a_(21)),(b_2,a_(22))|; D_1:=|(a_(11),b_1),(a_(12),b_2)|;`


Äquivalentes Gleichungssystem
`D*x_1 = D_1`
`D*x_2 = D_2`


Fallbaum
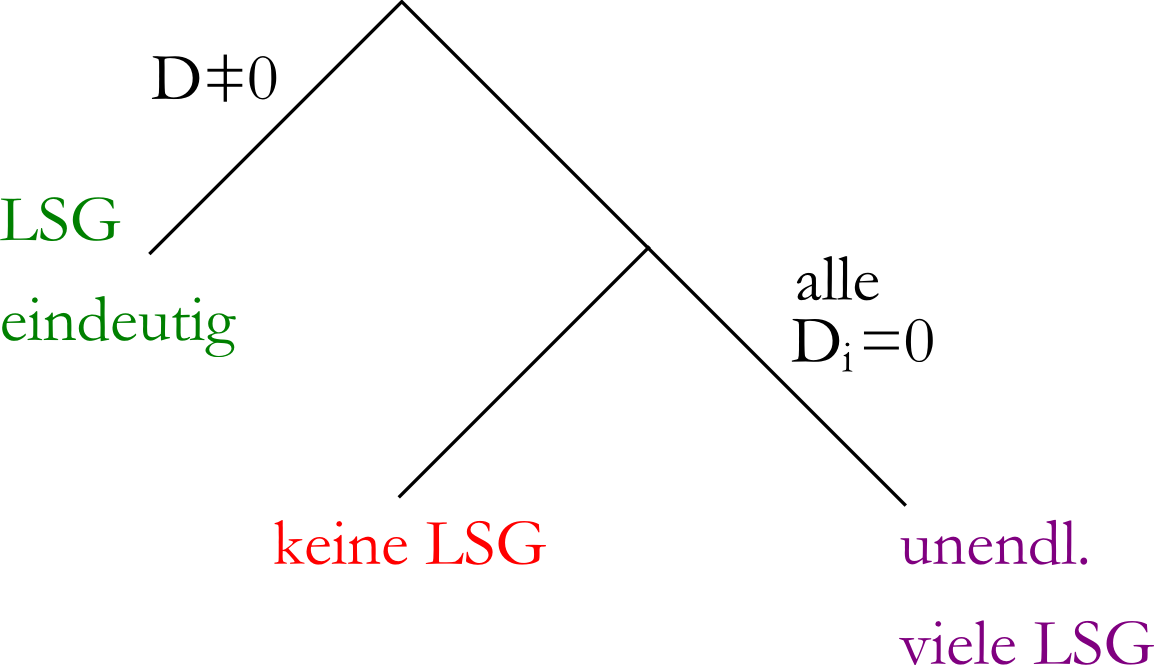
Zur Bestimmung der Lösungsmannigfaltigkeit untersucht man den Fallbaum:



Fallbaum zur Lösung eines 2x2-Systems
optimal sichtbar mit Firefox Formeln mit asciimath Druckversion