Galtonbrett
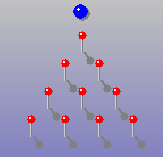
Einfaches Galtonbrett mit 4 Ebenen
| Versuchsbeschreibung |
- Die blaue Kugel soll über die Stecknadelreihe herabrollen.
- An jeder Stecknadel ist mit einer Wahrscheinlichkeit von 50% ein Fall nach links und mit 50% ein Fall nach rechts möglich
- nach Kollision mit einer Stecknadel aus der untersten Reihe sind 5 (nummeriert von 0 bis 4) verschiedene Endpositionen für die Kugel möglich
| Weg zur Wahrscheinlichkeitsverteilung |
- Verteilung schätzen lassen
- Experiment durchführen
- Verteilung systematisch untersuchen:
- alle Wege sind gleich wahrscheinlich
- die Wahrscheinlichkeit für einen Topf ergibt sich aus der Zahl der Wege, die zu diesem Topf führen
- bestimme also diese Zahl
- untersuche z.B. den Weg zum Topf 0:
er kann nur erreicht werden, wenn die Kugel an jeder Nadel nach links fällt {LLLL}, der Topf ist nur über diesen einen Weg erreichbar - die gleichen Überlegungen gelten für den Topf 4 (Symmetrie!)
- Topf 1 wird erreicht, wenn auf dem gesamten Weg genau einmal rechts abgebogen wird {RLLL},{LRLL},{LLRL} oder {LLLR}, das sind also 4 verschiedene Wege. Topf 3 genau umgekehrt.
- Topf 3 besitzt so viele Wege, wie man 2 L und 2 R in einem Wort anordnen kann: `Z = (4!)/(2!*2!) = 6`
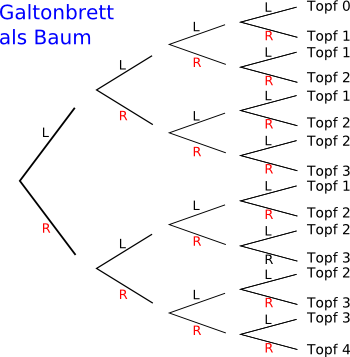
Baum zum Galtonbrett
| Allgemeine Verteilung |
`P(Topf k) = text(Anzahl Möglichkeiten k Rechtsabbiegungen auf den Weg zu verteilen)*0.5^k*0.5^(n-k)`
oder `P(k) = ((n),(k))*0.5^k*0.5^(n-k)`
Es ergibt sich also die Binomialverteilung für n, k und p=0.5.