Ideen zur Verwendung von Determinanten außerhalb der analyt. Geo


Dreiecksinhalt bei vorgegebenen Punkten nach "Lernen im Zusammenhang: Matrizen & Determinanten und Geometrie von Nicole Himmerlich und Tobias Leyh":Nicole Himmerlich und Tobias Leyh
Gegeben seien die Punkte `P_1(x_1|y_1), P_2(x_2|y_2) und P_3(x_3|y_3).
Der Flächeninhalt des zugehörigen Dreiecks errechnet sich aus der Formel:
`A = 1/2*|(x_1,y_1,1),(x_2,y_2,1),(x_3,y_3,1)|`


Beweis der Formel über drei Trapeze
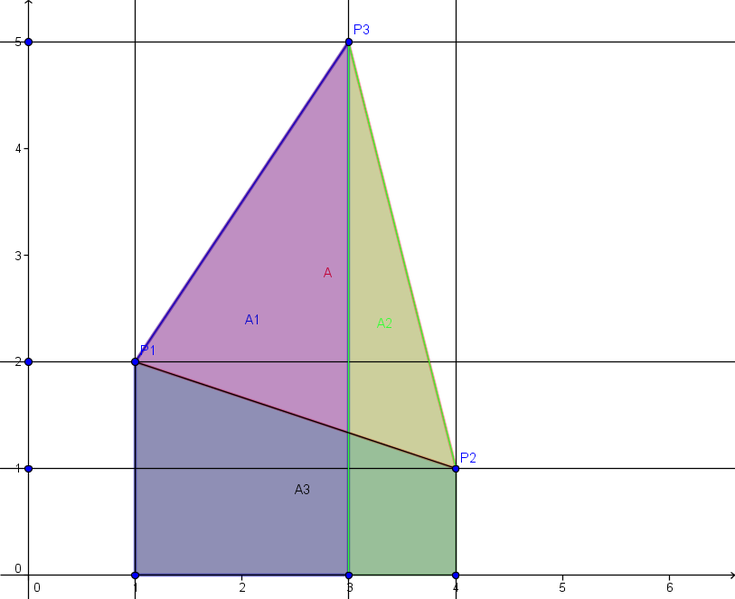
Der Flächeninhalt berechnet sich über `A_1+A_2-A_3`:



Dreiecksfläche über Trapezformeln

`A_1 = 1/2*(x_3-x_1)*(y_1+y_3)`
`A_2 = 1/2*(x_2-x_3)*(y_2+y_3)`
`A_3 = 1/2*(x_2-x_1)*(y_2+y_1)`
`-A_3 = 1/2*(x_1-x_2)*(y_2+y_1)`
`A_1+A_2-A_3 = 1/2*(x_1*(y_2-y_1-y_1-y_3)-x_2*(y_2+y_1-y_2-y_3)+x_3*(y_1+y_3-y_2-y_3) = 1/2*(x_1*(y_2-y_3)-x_2*(y_1-y_3)+x_3*(y_1-y_2))`
`= 1/2*|(x_1,y_1,1),(x_2,y_2,1),(x_3,y_3,1)|`