`x*sqrt x`

Definitionsmenge

Die Wurzel ist für negative Argumente nicht definiert. Deshalb gilt:
`D_f = RR_0^"+"`

Symmetrie

Da die Funktion im negative Bereich nicht definiert ist, kann keine Punkt- oder Achsensymmetrie zur y-Achse oder Nullpunkt existieren.

Nullstellen

`f(x) = 0` Ein Produkt ist dann Null, wenn einer seiner Faktoren Null ist:
1. Fall `x = 0`
2. Fall sqrt `x = 0 => x = 0`
Die einzige Nullstelle befindet sich bei x = 0

Waagerechte Tangenten

`f(x) = x*sqrt x = sqrt x * sqrt x * sqrt x = (sqrt x)^3 = x^(3/2)`
`f'(x) = 3/2*x^(1/2) = 3/2*sqrt x`
`f'(x) = 0 => x = 0`
Einzige Stelle mit waagerechter Tangente ist x = 0.

Monotonie

Die Wurzel ist für jedes Argument außer Null positiv definiert. Deshalb gilt:
`f'(x) > 0` für `x > 0`, also streng monoton steigend in `R^"+"`

Hochpunkte, Tiefpunkte

Waagerechte Tangente bei `x=0`
Streng monoton steigend für `x > 0`
`=> (0;0)` ist TIP und es existieren keine weiteren Extremstellen.

Flachpunkte

Bilde die zweite Ableitung:
`f''(x) = 1/2*3/2*x^(-(1/2)) = 3/(4*sqrt x)`
Gebrochen rationale Funktionen haben die Nullstellen dort, wo der Zähler Null und der Nenner nicht Null ist.
`3 ne 0 => ` keine Nullstellen der 2. Ableitung.

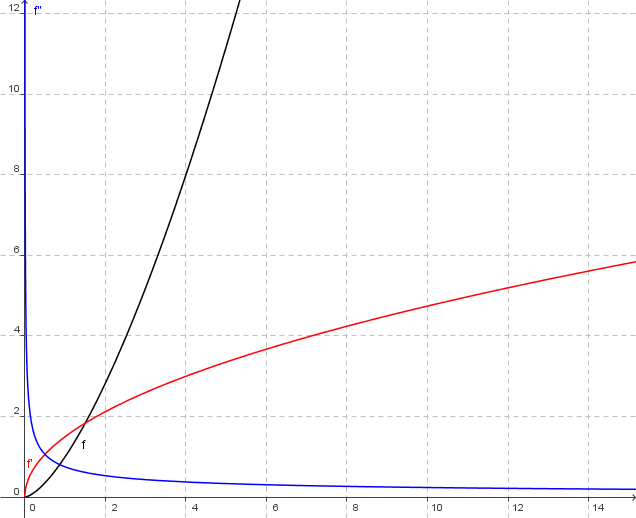
`x*sqrt x`