Lšnge von Vektoren
| Quaderdiagonale |
| Beispiel |
- Pythagoras "am Boden": `bar (OP') = sqrt(1^2+2^2)
- Pythagoras im Raumdreieck: `bar (OP) = sqrt( sqrt(1^2 + 2^2)^2 + 3^2 ) = sqrt( 1^2 + 2^2 + 3^2) = sqrt 14`
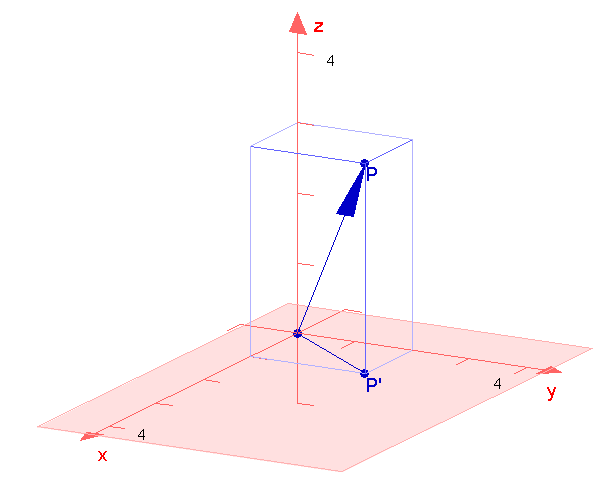
Lšnge eines Vektors als Quaderdiagonale
| UHU-Startseite►Mathematik►Jahrgangsstufen►11►Koordinatengeometrie im Raum►Anwendungen von Skalar- und Vektorprodukt► |
|
Lšnge von Vektoren
 Lšnge eines Vektors als Quaderdiagonale
|