UHU-Startseite►Mathematik►Jahrgangsstufen►11►Wahrscheinlichkeitsbegriff►
Vierfeldertafel in der Diagnostik


Aufgabe
Zur Untersuchung der Wirksamkeit eines Medikamentes schlucken 184 Personen ein Präparat (das Medikament `M` oder ein Placebo `bar M`). 121 Personen bekommen das tatsächliche Medikament verabreicht (`M`), bei 40 sind die Schmerzen nach 6h weniger als halb so stark (Wirksamkeit `W`), bei 55 Personen hat das Placebo keine Verbesserung (`bar W`) bewirkt.
  1. Erstellen Sie eine Vierfeldertafel für die absoluten Häufigkeiten
  2. Bestimmen Sie die relative Häufigkeit der Personen, bei denen das Placebo gewirkt hat und die relative Häufigkeit der Personen bei denen das Medikament gewirkt hat.
  3. Bestätigt die Studie die Wirksamkeit des Medikamentes?



Lösung
abs. H.keine Schmerzen nach 6h `W`Schmerzen nach 6h `bar W``Sigma`
Medikament `M`3289121
Placebo `bar M`85563
`Sigma`40144184



Das Medikament funktioniert, wenn nach Einnahme die Wirkung (also das Nachlassen der Schmerzen) größer ist als beim Placebo:
  • 63 Personen bekamen ein Placebo verarbreicht, davon hatten 8 nach 6h keine Schmerzen. Wirksamkeit: `8/63 = 12.7%`
  • 121 Personen bekamen das Medikament verabreicht, davon hatten 32 nach 6h keine Schmerzen. Wirksamkeit: `32/121 = 26.4%`, also der doppelte Prozentsatz.



Nochmals Vierfeldertafel
Rechnerische Variante bei gegebenen relativen Häufigkeiten:
abs. H.keine Schmerzen nach 6h `W`Schmerzen nach 6h `bar W``Sigma`
Medikament `M`18%48%66%
Placebo
`bar M`		4%30%34%
`Sigma`22%78%100%


$P(M \cap W) = 0,18$ (aus Tabelle)
$P(M) = 0,66 \quad P(W) = 0,22$ (Zeile, bzw. Spalte die zu M bzw. W gehören)
$P(M) \cdot P(W) = 0,1452 \ne 0,18 = P(M \cap W)$
Die Formel gilt nicht, die Ereignisse sind nicht stochastisch unabhängig.



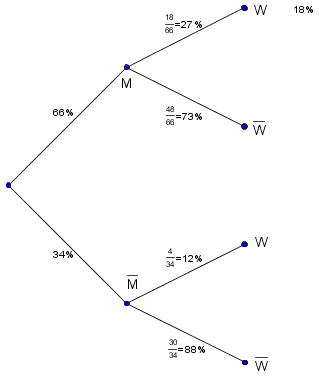
Medikamentenwirkung: Baum I
optimal sichtbar mit Firefox Formeln mit asciimath Druckversion