|
Beispiel Würfelbauten
| Ziel der folgenden Aufgaben |
- Durch exemplarisches Durchrechnen
- den Algorithmus erkennen
- und in allgemeiner Form (als TERM) aufschreiben
Untersuche eine zweistöckige Würfelmauer:
Wie viele sichtbare und unsichtbare Quadrate
gibt es bei 1, 2, 3, 4, 5, 6, ... x Basiswürfeln?
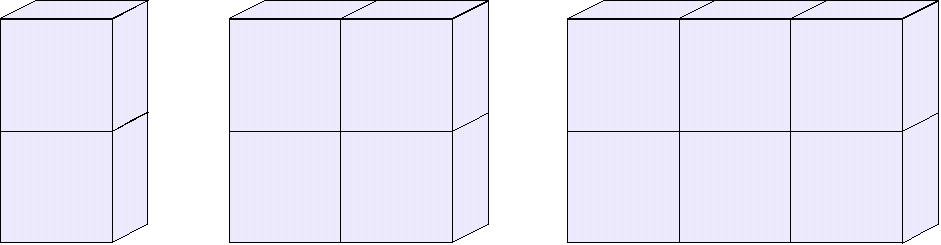
Zweistöckige Würfelmauer
| Lösung für die zweistöckige Würfelmauer |
| Basiswürfel |
verdeckte Seiten |
sichtbare Seiten |
| 1 | 3 | 9 |
| 2 | 10 | 14 |
| 3 | 17 | 19 |
| 4 | 24 | 24 |
| 5 | 31 | 29 |
| 6 | 38 | 34 |
| x | 7x-4 | 5x+4 |
Untersuche eine quadratische Würfelmauer:
Wie viele sichtbare und unsichtbare Quadrate
gibt es bei 1, 2, 3, 4, 5, 6, ... x Basiswürfeln?
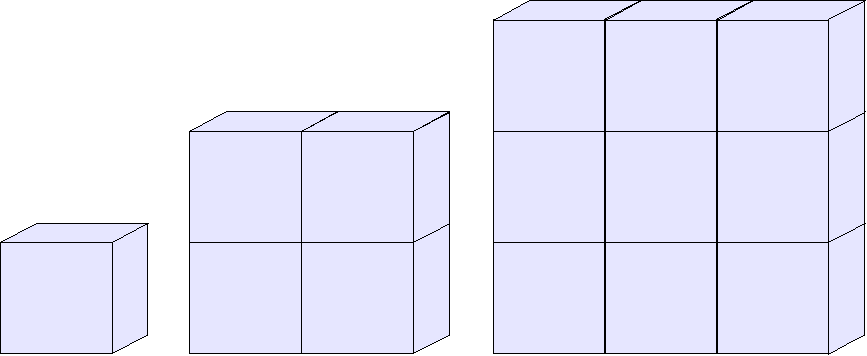
Quadratische Würfelmauer
| Lösung: Quadratische Würfelmauer |
| Basiswürfel |
verdeckte Seiten |
sichtbare Seiten |
| 1 | 1 | 5 |
| 2 | 10 | 14 |
| 3 | 27 | 27 |
| 4 | 52 | 44 |
| 5 | 85 | 65 |
| 6 | 126 | 90 |
| x | x + 4⋅x⋅(x-1) | 2x²+3x |
|

