Koordinatengleichung

Zuordnung von Raumpunkten

Gesucht ist ein einfaches Verfahren, um jeden Punkt des Raumes checken zu können, ob er ein Teil der Ebene ist.
Günstig wäre eine Gleichung für `x_1`, `x_2` und `x_3`.

Reduktion auf lineare Abhängigkeit

Eine mögliche Bedingung lässt sich dadurch erstellen, dass der Vektor vom Aufpunkt zum Testpunkt in der von `vec u` und `vec v` aufgespannten Ebene liegt:
`|vec X - vec A, vec u, vec v| = 0` alle drei Vektoren sind also nicht linear unabhängig.

Gegeben ist eine Ebene E mit Aufpunkt `vec A` und den Richtungsvektoren `vec u` und `vec v`
`vec X = ((x_1),(x_2),(x_3)) in E` wenn `|vec X - vec A, vec u, vec v| = 0`
Die sich ergebende Gleichung heißt Koordinatengleichung der Ebene.

Beispiel 1: Eine einfache Ebene

`E:vec X = ((0),(0),(2))+lambda*((1),(0),(0))+mu*((0),(1),(0))`.
Bestimmung der Koordinatengleichung:
`|vec X - vec A,vec u, vec v| = |(x_1-0,1,0),(x_2-0,0,1),(x_3-2,0,0| = 0 + x_3-2+0-0-0-0=x_3-2 = 0`

`x_3-2 = 0` ist also die Koordinatengleichung.

`x_1` und `x_2` dürfen also beliebig gewählt werden, wichtig ist nur, dass `x_3=2` ist.

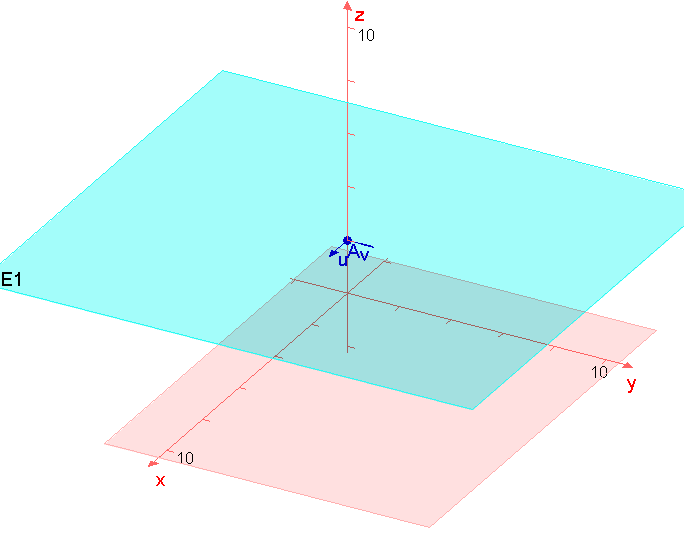
Zur Koordinatengleichung einer einfachen Ebene

Beispiel 2: eine andere Ebene

`E:vec X = ((0),(0),(2))+lambda*((1),(0),(-1))+mu*((0),(1),(-2))`.
Bestimmung der Koordinatengleichung:
`|vec X - vec A,vec u, vec v| = |(x_1-0,1,0),(x_2-0,0,1),(x_3-2,-1,-2| = `
`0 + x_3-2+0-(-1)*x_1-(-2)*x_2-0=x_3-2+x_1+x_2 = 0`

`x_1+2x_2+x_3-2 = 0` ist also die Koordinatengleichung.

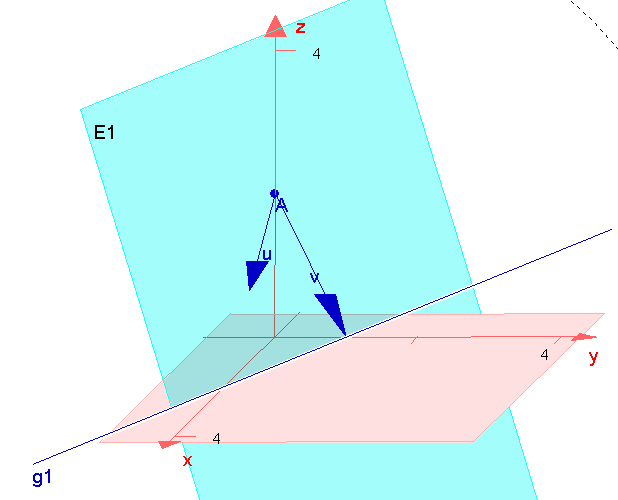
Zur Koordinatengleichung einer Ebene