|
Ebenengleichung
Die Menge aller Punkte `vec X` einer Ebene im Raum lässt sich mit Hilfe eines
- Aufpunktes `vec A` (beliebiger Punkt der Geraden),
- zweier Richtungsvektoren `vec u, vec v` (zeigen vom Aufpunkt in verschiedene Richtungen der Ebene)
- und zweier Parameter `lambda` und `mu`
beschreiben: `vec X = vec A + lambda*vec u + mu*vec v` mit `lambda, mu in RR`
`E: vec X = ((0),(0),(1))+lambda((1),(0),(-1))+mu*((0),(1),(-1))`
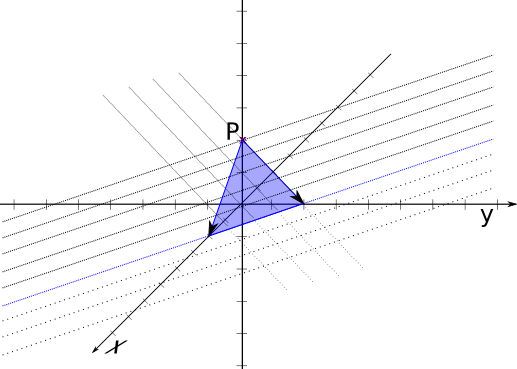
Beispielebene, gezeichnet
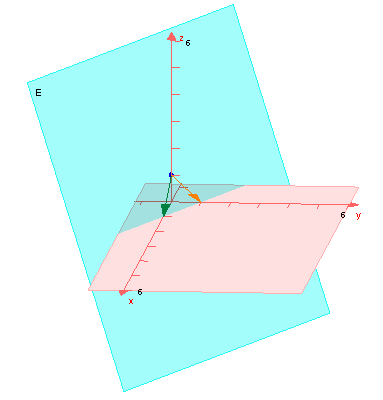
Beispielebene
- beide Richtungsvektoren fehlen
- Erzeugung durch Punkt-Verbindungsvektoren
| Ebene durch eine Gerade und einen Punkt |
- Ein Richtungsvektor fehlt
- Erzeugung durch Verbindungsvektor des Punktes und des Geradenaufpunktes
| Ebene durch zwei Parallelen |
- fehlt ein nicht-kollinearer Richtungsvektor
- Erzeugung durch Verbindungsvektor der beiden Geradenaufpunkte
| Ebene durch zwei sich schneidende Geraden |
- fehlt garnichts
- benutze einen Aufpunkt und die Richtungsvektoren der beiden Geraden
|

