Lösung mit Determinanten


Berechnung des Wertes einer Determinante
Die allgemeine dreidimensionale Determinante:
`|[a_1,b_1,c_1],[a_2,b_2,c_2],[a_3,b_3,c_3]|` berechnet man mit
  • Berechnungsformel A:
    `D = a_1*|[b_2,c_2],[b_3,c_3]| - a_2*|[b_1,c_1],[b_3,c_3]| + a_3*|[b_1,c_1],[b_2,c_2]|`
  • Berechnungsformel B (Sarrus):
    SOS - NOS (Südostsumme - Nordostsumme): `D = a_1b_2c_3+b_1c_2a_3+c_1a_2b_3-a_3b_2c_1-b_3c_2a_1-c_3a_2b_1`




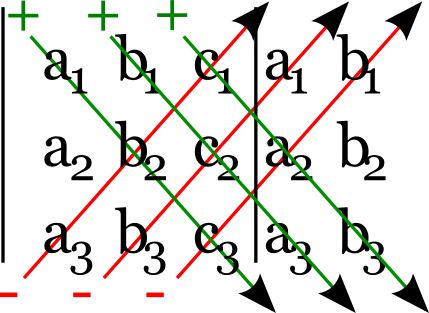
Berechnung des Wertes einer Determinante

Lösen eines (3,3)-Systems mit Hilfe von Determinanten
`a_(11)x_1+a_(21)x_2+a_(31)x_3=b_1`
`a_(12)x_1+a_(22)x_2+a_(32)x_3=b_2`
`a_(13)x_1+a_(23)x_2+a_(33)x_3=b_3`
`D := det(vec a_1, vec a_2, vec a_3)
`D_1 := det(vec b, vec a_2, vec a_3)
`D_2 := det(vec a_1, vec b, vec a_3)
`D_3 := det(vec a_1, vec a_2, vec b)
wenn `D != 0` dann gibt es drei Lösungen:
`x_1 = D_1/D; x_2 = D_2/D; x_3 = D_3/D`




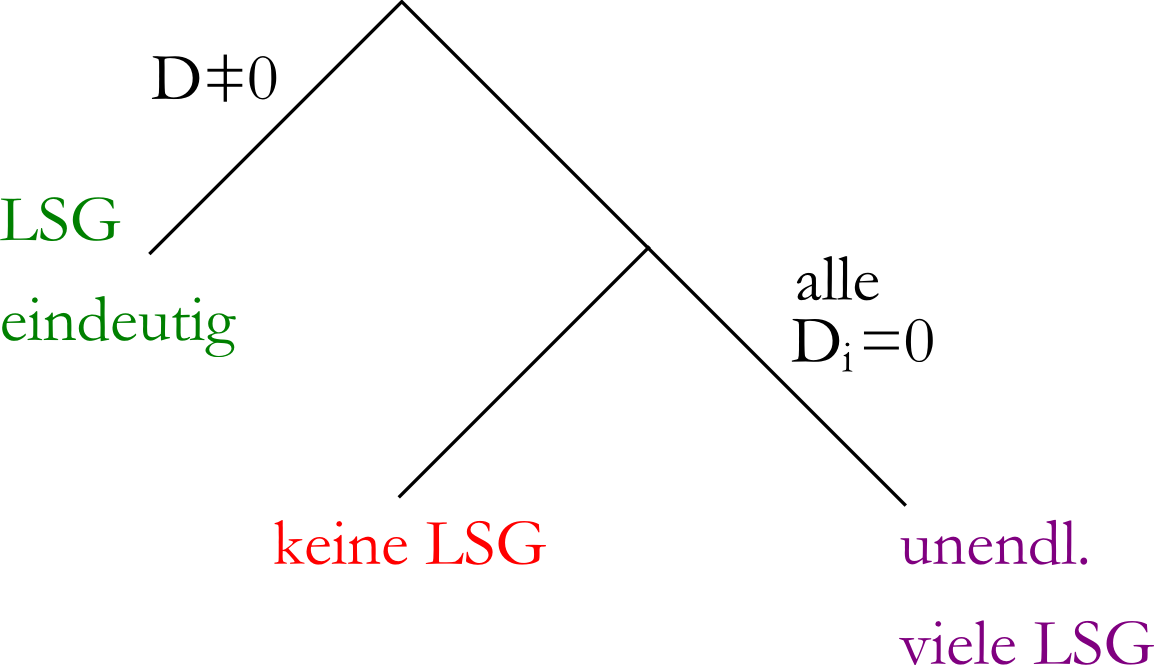
Determinanten-Fallbaum