Beweis zur Ableitungsfunktion über die Umkehrfunktion

Zusammenhang der Ableitungen von Funktion und Umkehrfunktion

Wie hier zu entnehmen besteht folgender Zusammenhang zwischen den Ableitungen von Funktion und Umkehrfunktion:
`(f^(-1))'(x) = 1/(f'(f^(-1)(x)))`
Diesen Zusammenhang kann man sich auch dadurch so klarmachen:

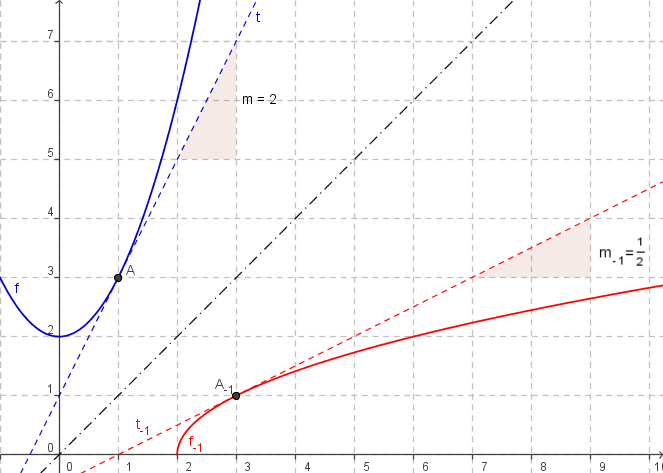
die Umkehrfunktion entsteht durch Spiegelung an der Winkelhalbieren
die Steigung `m = tan alpha` mit `alpha` Schnittwinkel zwischen Tangente und x-Achse
wird zu `m_(-1) = tan (90°-alpha) = cot(alpha) = 1/tan(alpha) = 1/m`

Jetzt müssen noch die Positionen der Tangenten berücksichtigt werden:

Tangente `t_(-1)(x)` im Punkt `(x_o|y_o)`
ergab sich durch Spiegelung der Tangente t im Punkt `(y_o|x_o)`

Beides zusammen:
`f^(-1)'(x_o) = 1/(f'(y_o)) = 1/(f'(f^(-1)(x_o)))`

Zur Ableitung der Umkehrfunktion

Ableitungsfunktion der Logarithmusfunktion

Wählt man
`f(x) = e^x => f'(x) = e^x` und
`f^(-1)(x) = ln(x)`

mit der Formel ergibt sich folgender Zusammenhang:

`ln'(x) = f^(-1)'(x) = 1/(f'(f^(-1)(x))) = 1/(e^ln(x)) = 1/x`