|
Einführung der ganzen Zahlen
Allgemein: Zur Erweiterung von Zahlbereichen
| Übergang zu den negativen Zahlen |
- rückwärts Zählen
- Zahlengerade: Thermometer in die Waagerechte legen
| Addition und Subtraktion in `ZZ` über Rechenreihen: Aspekte |
- Einfaches Bild der Rechenoperationen, das sich leicht erweitern lässt
- Expermimentieren spielt eine Rolle im Erarbeitungsprozess
| Addition und Subtraktion in `ZZ` über Rechenreihen: Vorgehensweise |
- Geometrische Interpretation von Addition und Subtraktion auf der Zahlengeraden:
Addition (Subtraktion) einer natürlichen Zahl bedeutet auf der Zahlengeraden von der Position
der ersten Zahl um den Betrag der zweiten Zahl nach rechts (links) gehen.
- Erweiterung der Regel durch Rechenreihen
(+5) + (+2) = +7
(+5) + (+1) = +6
(+5) + 0 = +5
(+5) + (-1) = +4
(+5) + (-2) = +3
(+5) - (+2) = +3
(+5) - (+1) = +4
(+5) - 0 = +5
(+5) - (-1) = +6
(+5) - (-2) = +7
-
Zusatz zur Regel:
Addition (Subtraktion) einer negativen Zahl bedeutet auf der Zahlengeraden von der Position der ersten Zahl um den Betrag der zweiten Zahl nach links(rechts) gehen.
-
Zusammenfassung
(+5) + (+2) = 7 = (+5) - (-2) (von 5 aus um zwei nach rechts)
(+5) - (+2) = 3 = (+5) + (-2) (von 5 aus um zwei nach links)
-
Abschließende Zusammenfassung
Treffen zwei gleiche Zeichen aufeinander, so können sie durch ein „Plus“ ersetzt werden, zwei
ungleiche Zeichen durch ein „Minus“
| Multiplikation und Division in `ZZ` über Rechenreihen |
(+3) · (+2) = +6
(+3) · (+1) = +3
(+3) · 0 = 0
(+3) · (-1) =(-1)+(-1)+(-1) = -3
(+3) · (-2) =(-2)+... = -6
(+2) · (+2) = +4
(+2) · (+1) = +2
(+2) · 0 = 0
(+2) · (-1) = -2
(+2) · (-2) = -4
K-Gesetz soll weiterhin gelten:
(-2) · (+3) = -6
(-2) · (+2) = -4
(-2) · (+1) = -2
(-2) · 0 = 0
(-2) · (-1) = +2
(-2) · (-2) = +4
| Zusammenfassung in einer exe-Datei |
Alle vorher behandelten Aspekte sind in diesem Programm eingearbeitet. Es eignet sich gut zur computergestützten Selbstaneignung des Stoffes.
| Addition und Subtraktion in `ZZ` über Wanderung auf der Zahlengeraden |
Addieren bedeutet: vorwärts gehen; Subtrahieren: rückwärts gehen
Ist die Zahl negativ, so muss man sich umdrehen;
(Basiert auf dem Vektormodell!)
Beispiel: +1 - (-2) = +3
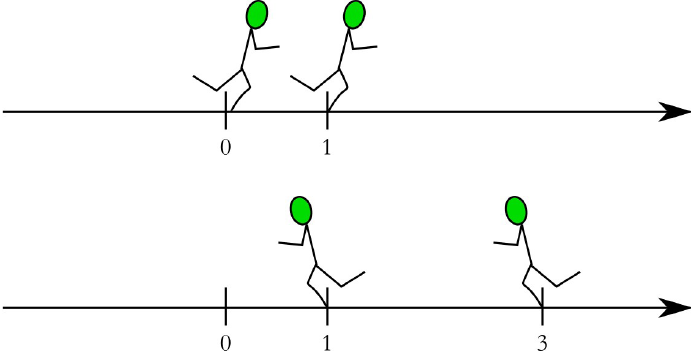
Subtraktion einer negativen Zahl
| Aspekte dieses Verfahrens |
- operativ erfahrbar: man kann es ausprobieren
Ein Busfahrer hat vor der letzten Station noch eine Person mit im Bus. Er bittet ihn, nach vorne zu kommen. Nachdem sich herausstellt, dass sie den gleichen Weg haben, nimmt der ihn der Fahrer noch bei der Ausrückfahrt mit. Es stellt sich heraus, dass der Fahrgast Mathematiker ist und nachdem sich der Busfahrer nicht so recht vorstellen kann, was man da so tut erklärt ihm der Mathematiker folgende Rechnung: 'Sie haben 5 und jetzt nehmen Sie acht weg', 'aber das geht doch gar nicht', 'doch, wir Mathematiker haben herausgefunden, dass man diese Zahl als -3 schreiben kann und wenn ich jetzt 3 addiere erhalte ich 0', 'das ist ja interessant!'. Abends kommt der Busfahrer nach Hause und erzählt seiner Frau von seinem Tag und von der Begegnung mit dem Mathematiker: 'Stell dir vor, wenn ich 5 Leute im Bus habe und es steigen 8 aus, ', 'aber das geht doch gar nicht', 'doch, wenn an der nächsten Station drei einsteigen, dann ist keiner mehr im Bus!'.
|
