andere Asymptoten
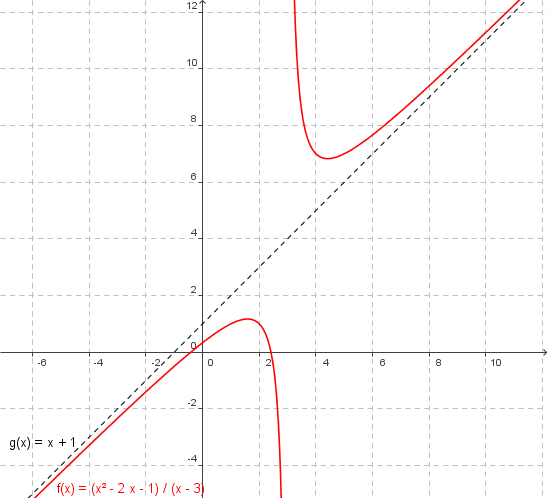
lineare Asymptote
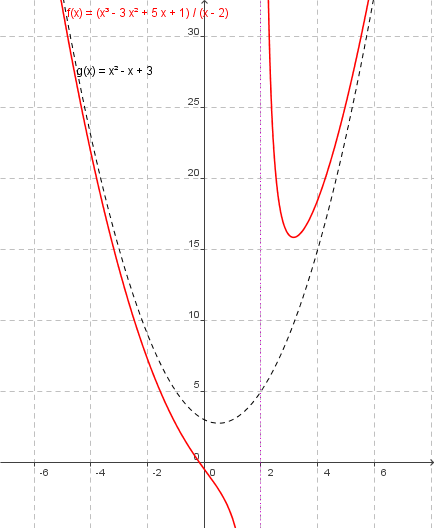
Quadratische Asymptote
| Graph im Bereich von großen Zahlen |
- Der Graph einer gebrochen rationalen Funktion nähert sich bei großen Zahlen dem Graphe einer rationalen Funktion an.
- Um den Funktionsterm für diese "Annäherungsfunktion" zu erhalten muss die Darstellung des Terms umgeformt werden.
| Gebrochen rationale Funktion als Summe |
- Darstellung der Funktion als eine Summe aus "wachsendem" und "verschwindendem" Teil
- mit Hilfe der Polynomdivision ergibt sich ein ganzrationales Polynom und ein Rest
| Beispiele mit linearer Asymptote |
Polynomdivision:
x² - 2x - 1 : (x-3) = x + 1 + 2/(x-3)
x² - 3x
-------
x - 1
x - 3
-----
2
asymptotische Funktion: `a(x) = x + 1`
| Beispiel mit quadratischer Asymptote |
Polynomdivision:
x³ - 3x² + 5x + 1 : (x-2) = x² - x + 3 + 7/(x-2)
x³ - 2x²
--------
- x² + 5x
- x² + 2x
---------
3x + 1
3x - 6
------
7