Geradengleichung
Die Menge aller Punkte `vec X` einer Geraden im Raum lässt sich mit Hilfe eines
- Aufpunktes `vec G` (beliebiger Punkt der Geraden),
- eines Richtungsvektors `vec v` (zeigt vom Aufpunkt in Richtung der Geraden)
- und eines Parameters `lambda` (dessen Wert sämtliche reellen Zahlen annehmen kann)
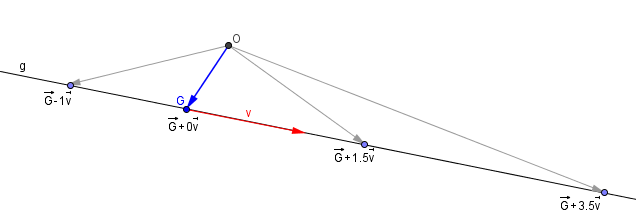
Gerade mit der Darstellung verschiedener Punkte
| Anmerkungen |
- Diese Beschreibung einer Geraden heißt auch Parameterform oder Punkt-Richtungs-Form
- `vec v != vec 0`
- eine Gerade lässt sich, je nach Aufpunkt, durch verschiedene Gleichungen beschreiben
- man sucht besonders einfache Beschreibungen (wie das Kürzen bei Brüchen):
`vec X = ((1),(2),(3)) + lambda*((400),(0),(200)) = ((1),(2),(3)) + lambda*((2),(0),(1))`
die zweite Darstellung zeigt in die gleiche Richtung, ist aber einfacher vorzustellen.