Beschreibung von Laserstrahlen im Raum



Viele Laser fokussieren auf ein Objekt im Raum

Abstraktion in die Mathematik
  • Der Laser kann gut durch eine Halbgerade modelliert werden
  • Um die alle Raumpunkte zu beschreiben, die zu einer Halbgerade gehören, benötigt man einen Startpunkt und einen Vektor.
  • Der Vektor gibt die Raumrichtung des Strahls an. Um jeden Punkt der Halbgerade erreichen zu können, muss die Vektorlänge beliebig einstellbar sein.




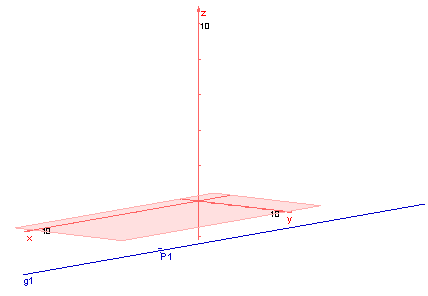
Eine Gerade im Raum

Ein einfaches Beispiel
Beschreibung der Menge aller Punkte des Raumes, die durch eine Halbgerade in x-Richtung mit Startpunkt `P = ((4),(3),(-2))` festgelegt sind:
`vec x = ((4),(3),(-2)) + lambda*((1),(0),(0))` mit `lambda in RR_0^text(+)`.
Durch Variation von `lambda` erhält man verschiedene Punkte der Gerade:
  • `lambda = 0 => vec X = ((4),(3),(-2))` ist genau der Startpunkt und muss deshalb auf der Halbgeraden liegen.
  • `lambda = 1 => vec X = ((5),(3),(-2))` dieser Punkt liegt genau 1 von `vec P` in x-Richtung entfernt und gehört somit zur Geraden.
  • `lambda = 100 => vec X = ((104),(3),(-2))` liegt 100 Einheiten in x-Richtung von P entfernt, also wiederum auf der gewünschten Halbgeraden.



Aufgabe zur Laserstation
angenommen, in der oben dargestellten Szene liegt der Ursprung genau in der Mitte der Lasersquellen, die mit Radius 5 vom Ursprung entfernt liegen.
Berechnen Sie 4 Halbgeraden für Laser, die sich in einer Höhe 5 über dem Ursprung treffen.


Lösung
`vec X_1 = ((5),(0),(0))+lambda*((-1),(0),(1))`
`vec X_1 = ((-5),(0),(0))+lambda*((+1),(0),(1))`
`vec X_1 = ((0),(5),(0))+lambda*((0),(-1),(1))`
`vec X_1 = ((0),(-5),(0))+lambda*((0),(+1),(1))`