UHU-Startseite►Mathematik►Jahrgangsstufen►10►Kreis►Berechnungen an Figuren die elementare Kreisteile enthalten►
Berechnungen zum Gotthard-Basistunnel


Über den Tunnel
Dieser Tunnel soll einmal eine schnelle Eisenbahnverbindung durch die Schweiz ermöglichen. Dazu werden zwei 75 km lange Röhren (mit dem Durchmesser 8,80m) durch den Fels getrieben. Anschließend wird der Boden geebnet und die Zugtrasse installiert. Mehr zum Thema gibt es hier.



Blick in den Gotthard-Basistunnel


Modell des Tunnelquerschnittes

Aufgaben
  1. Wieviel Kubikmeter Gestein wird mindestens aus den Tunnelröhren gebohrt?
  2. Zeigen Sie anhand der Grafik: Es müssen etwa 430 000m³ Material eingebracht werden, um den Boden für die Eisenbahntrasse zu legen.
  3. Wie viele Kubikmeter Luft werden sich daher im fertigen Tunnelbau befinden?



Tipps I
  1. Gefragt ist hier das Volumen eines Zylinders.
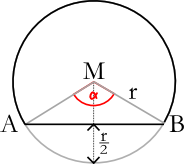
Zur Lösung der weiteren Aufgaben muss der Winkel `alpha` bestimmt werden. Die Abstraktion lässt sich durch zeichnen zweier Hilfslinien zu einer Figur aus zwei Dreiecken ergänzen.
    • Gesucht ist die Querschnittsfläche zwischen der waagerechten Strecke und dem Boden des Kreises (Fläche des Kreissegmentes)
    • Berechnen lässt sich die Fläche des Dreiecks `Delta ABM` und die Fläche des Tortenstückes (Kreissektors) `AMB`
    • Deren Differenz ergibt die gesuchte Fläche (Fläche des Kreissegmentes).
  2. Der restliche Teil des abstrahierten Tunnels ist mit Luft gefüllt.




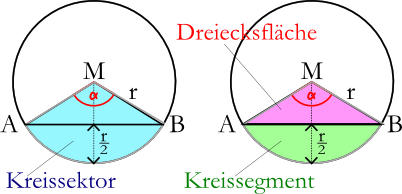
Abstraktion des Tunnelquerschnittes

Tipps II
  1. Das Zylindervolumen berechnet sich zu `V = G*h` mit `G = r^2*pi`
Zur Bestimmung von `alpha`:



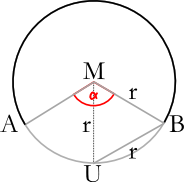
Abstrahierter Tunnelquerschnitt mit Bestimmung des Winkels

    • Der Flächeninhalt des Dreiecks `Delta ABM` entspricht dem Flächeninhalt des dargestellten gleichseitigen Dreiecks `Delta MUB`.
    • Der Flächeninhalt des gleichseitigen Dreiecks berechnet sich zu `A_"gleichseitig" = sqrt 3/4*r^2`
    • Der Flächeninhalt des Kreissektors macht einen bestimmten Anteil des gesamten Kreisflächeninhaltes aus: `A_"Sektor"/A_"Kreis" = alpha/(360°)`



Lösungen
  1. `V=G*h=r^2*pi*h = (4.4m)^2*pi*75000m ~~ 4560000m³`
  2. `alpha = 2*60° = 120°`
    `A_"Segment" = A_"Sektor" - A_"Dreieck" = (120°)/(360°)*pi*(4.4m)^2 - sqrt 3/4*(4.4m)^2 ~~ 20.2 m^2 - 14.5 m^2 = 5.7 m^2`
    `5.7 m^2*75000m ~~ 432 000 m^3`
  3. `4560000m^3 - 432000m^3 ~~ 4130 000m^3`


optimal sichtbar mit Firefox Formeln mit asciimath Druckversion