Rechnerische Überprüfung in 3D


Determinante in 3D
Die allgemeine dreidimensionale Determinante:
`|[a_1,b_1,c_1],[a_2,b_2,c_2],[a_3,b_3,c_3]|` berechnet man mit
  • Berechnungsformel A:
    `D = a_1*|[b_2,c_2],[b_3,c_3]| - a_2*|[b_1,c_1],[b_3,c_3]| + a_3*|[b_1,c_1],[b_2,c_2]|`
  • Berechnungsformel B (Sarrus):
    SOS - NOS (Südostsumme - Nordostsumme): `D = a_1b_2c_3+b_1c_2a_3+c_1a_2b_3-a_3b_2c_1-b_3c_2a_1-c_3a_2b_1`




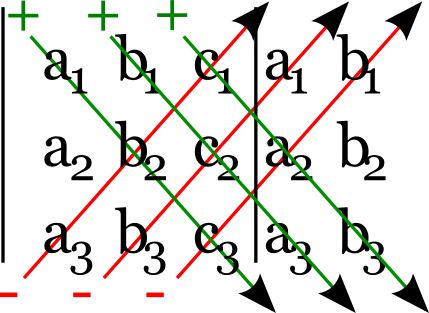
SOS-SWS-Regel

Berechnung der linearen (Un-)abhängigkeit
Drei Vektoren `vec a`, `vec b` und `vec c` sind linear unabhängig, wenn `D(vec a, vec b, vec c) = |[a_1,b_1,c_1],[a_2,b_2,c_2],[a_3,b_3,c_3]| != 0`,
und linear abhängig (komplanar oder kollinear), wenn `D = 0`



Beispiel
Untersuche auf Komplanarität:
`vec a = ((1),(-2),(5)); vec b = ((2),(3),(1)); vec c = ((3),(8),(-3));`

Untersuchung der Determinante:
`|[1,2,3],[-2,3,8],[5,1,-3]| = 1*(3*(-3)-1*8) + 2*(2*(-3)-1*3) + 5*(2*8-3*3) = 1*(-9-8) + 2*(-6-3)+5*(16-9) = -17 -18 + 35 = 0`
Die Vektoren sind also linear abhängig!


Berechnung ohne Determinante
Überprüfen, ob `vec a` eine Linearkombination aus `vec b` und `vec c` ist, wenn `vec b` und `vec c` nicht kollinear sind:

`vec b != lambda*vec c`, da man die erste Koordinate mit `3/2`, die zweite aber mit `8/3` multiplizieren müsste.
Überprüfung, ob `vec a` eine Linearkombination aus `vec b` und `vec c`:
`((1),(-2),(5))=lambda*((2),(3),(1))+mu*((3),(8),(-3))` oder

`1 = 2*lambda + 3*mu`
`-2 = 3*lambda + 8*mu`
`5 = lambda - 3*mu`
wenn sich `lambda` und `mu` finden lassen, dann sind alle Vektoren komplanar: