Rechnerische Überprüfung in 2D

Lineare Abhängigkeit im 2-dimensionalen Raum

2 Vektoren `vec a` und `vec b` sind im 2-dimensionalen Raum voneinander linear abhängig, wenn

sie die Ebene nicht aufspannen können (es Punkte der Ebene gibt, die über keine Linearkombination von `vec a` und `vec b` erreichbar sind
entlang der gleichen Raumrichtung zeigen
es ein `lambda!=0` und `mu!=0` gibt, so dass `lambda vec a + mu vec b = vec o`

Bedeutung für die Koordinaten der Vektoren

2 Vektoren `vec a` und `vec b` sind voneinander linear abhängig.
Welche Bedingung gilt dann zwischen den Koordinaten `a_1`, `a_2`, `b_1` und `b_2`?
`vec o = lambda vec a + mu vec b` bedeutet:

`0 = lambda a_1 + mu b_1` (A) und
`0 = lambda a_2 + mu b_2` (B)

Zur Lösung müssen `lambda` und `mu` berechnet werden. Also auflösen von (A) nach `lambda`:
`lambda = -mu * b_1/a_1` und einsetzen in (B):

`0 = -mu*b_1/a_1*a_2 + mu*b_2 = mu*(b_2 - b_1/a_1*a_2)`
Da `mu` im Normalfall nicht Null ist, muss die Klammer Null werden um die Gleichung sicher immer zu erfüllen:

`b_2 - b_1/a_1*a_2 = 0` oder schöner: `a_1*b_2 - a_2*b_1 = 0`

Zwei Vektoren sind in der Ebene linear abhängig oder kollinear, wenn gilt:
`a_1*b_2 - a_2*b_1 = 0`

Determinante als Konstruktion

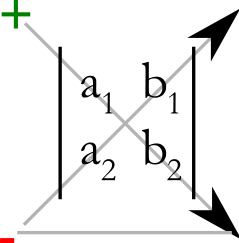
Damit man sich das leichter merken kann, ordnet man die Koordinaten in einer sogenannten Determinante an: `|[a_1,b_1],[a_2,b_2]| = 0` wobei man die Determinante so berechnet:

2-dimensionale Determinantenformel