Streckenteilung

Aufhänger: Goldener Schnitt

Teilt man eine Strecke so in zwei Teile a und b, das gilt:
`a/b = (a+b)/a`, dann ist sie im goldenen Schnitt geteilt.

Der vitruvianischen Mensch.

Definition

Gegeben ist die Gerade PQ mit `P!=Q`.

Liegt `T!=Q` auf der Geraden PQ, dann teilt T die Strecke [PQ] im Verhältnis `tau = bar(PT) : bar(TQ)`.
Wenn T außerhalb [PQ] liegt, dann wird `tau` negativ definiert.

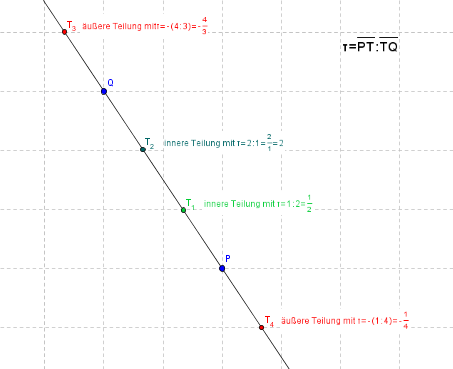
Beispiele für Streckenteilung

Vektor zum Teilpunkt