UHU-Startseite►Mathematik►Jahrgangsstufen►12►Binomialverteilung und Anwendung►Signifikanztests►
Einführungsbeispiel


Spinnt der Würfel?
Bei einem Mensch-ärgere-dich-Spiel, stellst du fest, dass du im Nachteil bist, weil dein Würfel kaum Sechser würfelt. Alle anderen behaupten, dass es sich aber um einen ganz normalen Würfel handelt, er sogar eher mehr Sechser würfelt.
Nullhypothese `H_0: p >= 1/6`

Stichprobe Zur Überprüfung würfelst du 10 mal und zählst die Anzahl der auftretenden Sechser.

Binomialverteilung:



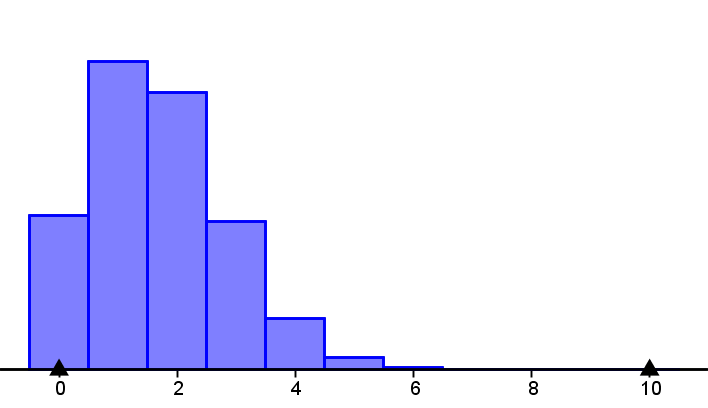
Binomialverteilung: Sechser bei 10xWürfeln

Entscheidungsregel Wenn bei zehn Würfen eine oder mehr Sechser fallen, dann ist der Würfel in Ordnung, sonst nicht.
`A = {1..10};   bar A = {0}`

Fehlerwahrscheinlichkeit Die Wahrscheinlichkeit für einen Fehler 1. Art (`alpha`) ist
`alpha = P_(1/6)^10(X=0) = (5/6)^10 approx 0,1614`

Mit einer Wahrscheinlichkeit von 16% wird ein normaler Würfel als fehlerhaft angesehen.


Europawahl
Im Polizeibericht steht: Die Zahl der Raser hat sich signifikant erhöht. Welcher Test könnte diese Aussage geliefert haben?


Beantwortung
  • z.B. bisher p('Raser') = 10%.
  • (Gegen)Hypothese `H_0`: p('Raser, heute') `le` 10%
  • gesucht ist der Ablehnungsbereich bei z.B. 100 Kontrollen: `B(100;0.1;Z ge k) le 5%` (die 5% sind das Signifikanzniveau)
  • `B(100;0.1;Z ge 16) = 3,99%`
  • `B(100;0.1;Z ge 15) = 7,26%`
  • mit k = 16 ergibt sich
  • `bar A = {16..100}` (Ablehnungsbereich)
  • Wenn also mehr als 15 auf 100 Raser gemessen wurden, dann hat sich mit 95% Sicherheit die Zahl der Raser erhöht.
optimal sichtbar mit Firefox Formeln mit asciimath Druckversion