Vektoren als Kombination aus Basisvektoren

Vektoren als Kombination aus Basisvektoren

Darstellung beliebiger Vektoren

Beispiel der Pfeil, der

vom Ursprung zum Punkt P(1|2|3) zeigt
ist ein Repräsentant eines Vektors `vec p`
der sich als Summe `vec p = 1* vec(e_1) + 2* vec(e_2) + 3* vec(e_3)` schreiben lässt

Jeder Vektor kann als Repräsentant einen Pfeil vom Ursprung aus haben
dieser Pfeil zeigt auf einen Punkt `P(p_x|p_y|p_z)` des KOSY
der entsprechende Vektor heißt Ortsvektor
und lässt sich darstellen durch:
`vec p = p_x*vec(e_1) + p_y * vec(e_2) + p_z * vec(e_3)`

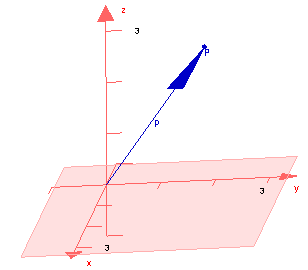
Linearkombination von Vektoren

Spaltendarstellung

Jeder Vektor lässt sich als eine Summe aus Vielfachen von Basisvektoren darstellen `vec a = a_1*vec(e_1)+a_2*vec(e_2) + a_3*vec (e_3)`.
`a_1,a_2,a_3` heißen Koordinaten des Vektors
Die Projektion auf die Achsen: `a_1*vec(e_1), a_2*vec(e_2), a_3*vec (e_3)` heißen Komponenten des Vektors

Zur Abkürzung führt man folgende Schreibweise ein:
`vec a = ((a_1),(a_2),(a_3))`

Beispiele

Vektor der Länge 3, parallel zur x-Achse: `vec a = ((3),(0),(0))`
Winkelhalbierender Vektor der xy-Ebene der Länge 1 `vec b = ((sqrt 2/2),(sqrt 2/2),(0))`
Spiegelvektor zum Vektor `e_3` `vec c = ((0),(0),(-1))
Ein senkrechter Vektor auf der yz-Ebene `vec d = ((-4),(0),(0))