|
Basisvektoren
| Übertragen des KOSY in ein Vektorsystem |
Um die Vorteile der Vektorrechnung in einem normalen KOSY nutzen zu können, müssen dessen grundlegenden Eigenschaften in die Vektorrechnung integriert ("verheiratet") werden.
Die Basisvektoren `vec(e_1), vec(e_2), vec(e_3)` sind die Vektoren der Länge 1 in Richtung der Koordinatenachsen x, y und z.
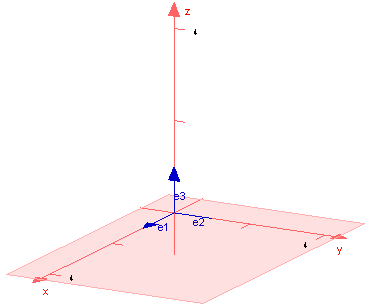
Basisvektoren
| Vektoren als Kombination aus Linearvektoren |
Aus diesen drei Vektoren lassen sich neue Vektoren bilden, z.B.
`vec u = 1 * vec(e_1) - 2 * vec(e_2) + 7 * vec (e_3)`
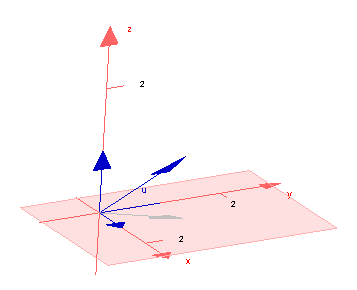
u=e1+e2+e3
|

