|
Übersicht: Rechnen mit Vektoren
| `vec(PQ)+vec(QR) = vec(PR)` oder vom Fuß des ersten zur Spitze des zweiten |
| `vec u + vec v = vec v + vec u` |
| `(vec u + vec v) + vec w = vec u + (vec v + vec w)` |
| Nullvektor: `vec o` (Länge 0, keine Richtung) |
|
Der Vektor der zu `vec a` addiert `vec o` ergibt heißt Gegenvektor `- vec a`
|
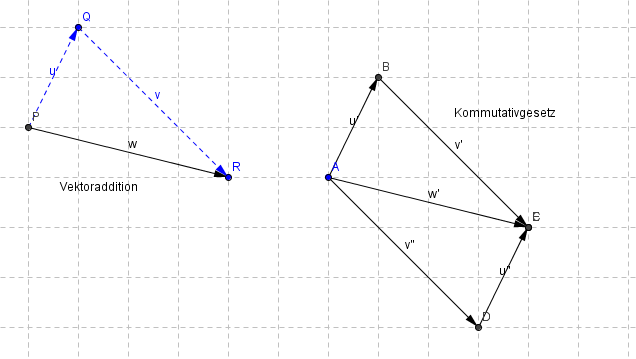
Vektoraddition und Kommutativgesetz
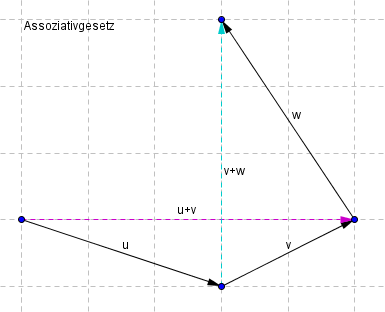
Assoziativgesetz der Vektoraddition
| `r*vec v` ist ein Vektor mit gleicher Richtung wie `vec v`, aber r-facher Länge. Für r < 0 wird der Gegenvektor der |r|-fachen Länge genommen. |
| `r*(s*vec v) = (r*s)*vec v` |
| `(r+s)*vec v = r* vec v + s* vec v` |
| `r*(vec v + vec w) = r* vec v + r* vec w` |
|

