UHU-Startseite►Mathematiklehrer►im Schulleben►Prüfungsorganisation►
zu prüfende Kompetenzen



Kompetenzmodell zur Erstellung von Aufgaben

Inhaltsbezogene Kompetenzen
  • Diese Leitideen versuchen die Phänomene zu erfassen, die man sieht, wenn man die Welt (auch die unserer Gedanken und Ideen) mit mathematischen Augen betrachtet
  • Die Leitideen entsprechen grob den Strängen des bayerischen Lehrplans in Mathematik.
  • Sie bilden unterschiedliche inhaltliche Schwerpunkte, denen der Mathematikstoff in der Schule gut zugeordnet werden kann.



Allgemeine Kompetenzen
  • K1 Mathematisch argumentieren (A)
  • K2 Mathematisch Probleme lösen (P)
  • K3 Mathematisch modellieren (M)
  • K4 Mathematische Darstellungen verwenden (D)
  • K5 Symbolisch, formal, technisch arbeiten können (F)
  • K6 Mathematisch kommunizieren (K)



Kompetenzen und Anforderungsbereiche
Argumentieren Problem lösen Modellieren
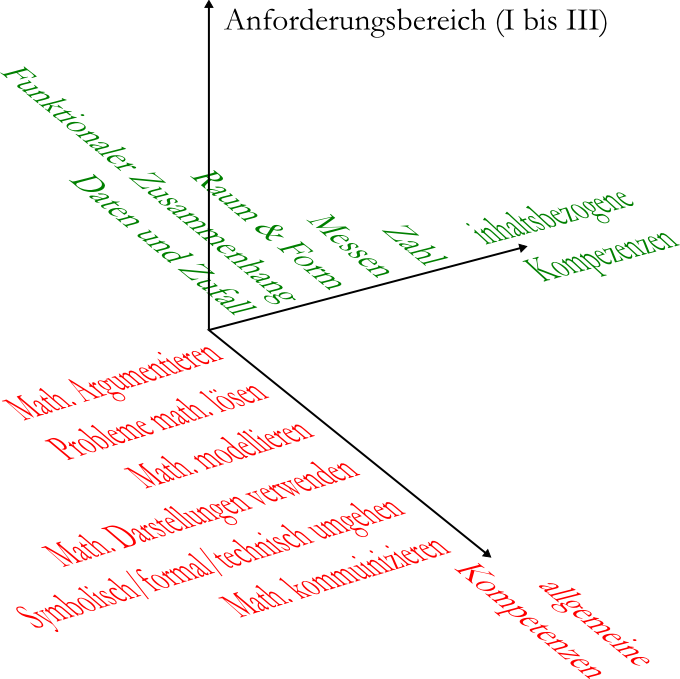
I Routineargumentationen (bekannte Sätze, Verfahren, Herleitungen usw.) wiedergeben und anwenden; einfache rechnerische Begründungen geben; mit Alltagswissen argumentieren Lösen einer einfachen mathematischen Aufgabenstellung durch Identifikation und Auswahl einer naheliegenden Strategie (z.B. Zeichnen einer einfachen Hilfslinie). Vertraute und direkt erkennbare Standardmodelle nutzen (z.B. Dreisatz); direktes Überführen einer Realsituation in die Mathematik; direktes Interpretieren eines mathematischen Resultats.
II Überschaubare mehrschrittige Argumentationen nachvollziehen, erläutern oder entwickeln Finden eines Lösungsweges zu einer Problemstellung durch ein mehrschrittiges strategiegestütztes Vorgehen. Mehrschrittige Formulierungen innerhalb weniger und klar formulierter Einschränkungen vornehmen; Ergebnisse einer solchen Modellierung interpretieren; ein mathematisches Modell passenden Realsituationen zuordnen oder an veränderte Umstände anpassen.
III Komplexe Argumentationen nutzen, erläutern oder entwickeln; verschiedene Argumente nach Kriterien wie Reichweite und Schlüssigkeit bewerten. Konstruieren einer elaborierten Strategie, um z.B. die Vollständigkeit einer Fallunterscheidung zu begründen oder eine Schlussfolgerung zu verallgemeinern; Reflektieren über verschiedene Lösungswege. Ein Modell zu einer komplexen Situation bilden, bei der die Annahmen, Variablen, Beziehungen und Einschränkungen neu definiert werden müssen; Überprüfen, Bewerten und Vergleichen von Modellen.
Darstellungen verwenden Symbolisch/formal/technisch rechnen kommunizieren
I Standarddarstellungen von mathematischen Objekten anfertigen und nutzen. Verwenden elementarer Lösungsverfahren; direktes Anwenden von Formeln und Symbolen; direktes Nutzen einfacher mathematischer Werkzeuge (z.B. Formelsammlung; Taschenrechner). Darlegung einfacher mathematischer Sachverhalte; Identifikation und Auswahl von Informationen aus kurzen mathematikhaltigen Texten (die Ordnung der Informationen im Text entspricht weitgehend den Schritten der mathematischen Bearbeitung)
II Gegebene Darstellungen verständig interpretieren oder verändern; zwischen zwei Darstellungen wechseln. Mehrschrittige Anwendung formal mathematischer Prozeduren; Umgang mit Variablen, Termen Gleichungen und Funktionen im Kontext; mathematische Werkzeuge je nach Situation und Zweck gezielt auswählen und einsetzen. Verständliche i.d.R. mehrschrittige Darlegung von Lösungswegen, Überlegungen und Ergebnissen; Äußerungen (richtige, aber auch fehlerhafte) von anderen Personen zu mathematischen Texten interpretieren; Identifikation und Auswahl von Informationen aus mathematikhaltigen Texten(Ordnung entspricht nicht den Bearbeitungsschritten).
III Unvertraute Darstellungen verstehen und verwenden; eigene Darstellungen problemadäquat entwickeln; verschiedene Formen der Darstellung zweckgerichtet beurteilen. Durchführen komplexer Prozeduren; Bewerten von Lösungs- und Kontrollverfahren; Reflektieren der Möglichkeiten und Grenzen mathematischer Werkzeuge. Entwickeln einer kohärenten und vollständigen Präsentation eines komplexen Lösungs- und Argumentationsprozesses; komplexe mathematische Texte sinnentnehmend erfassen; Äußerungen von anderen vergleichen, bewerten und ggf. korrigieren.




Kompetenztabelle
optimal sichtbar mit Firefox Formeln mit asciimath Druckversion