Senkrechte Asymptoten
| Definitionslücken |
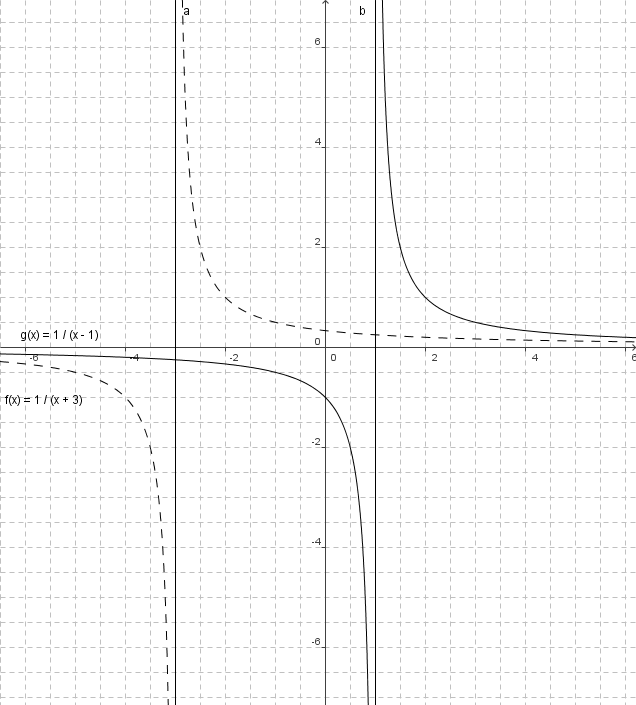
Senkrechte Asymptoten
| Untersuchung an der Definitionslücke |
`f(-2.5) = 2`
`f(-2.9) = 10`
`f(-2.99) = 100`
Der Graph steigt bei Annäherung an -3 stark an:
`lim_(x->3+0)->+oo`
| Stetig hebbare Definitionslücken |
schaut auf den ersten Blick der oberen Funktion ähnlich. Aber `f(-2.5) = -5.5`
`f(-2.9) = -5.9`
`f(-2.99) = - 5.99`
denn der Graph ist nicht der einer echt gebrochen rationalen Funktion:
`f(x) = ((x+3)(x-3))/(x+3)`
`g(x) = bar(f(x)) = x-3` heißt stetige Fortsetzung von f.
| Zusammenfassung: Asymptoten und Definitionslücken |
Besitzt eine Funktion Definitionslücken aufgrund von Nullstellen des Nenners, so ergibt sich eine
- hebbare Definitionslücke, wenn sich der Term mit der Nullstelle des Nenners kürzen lässt
- senkrechte Asymptote, wenn das nicht der Fall ist
| Vorgehensweise |
- Bestimme Nullstellen des Zählers und des Nenners
- Pole (mit senkrechten Asymptoten) sind Nullstellen des Nennerpolynoms, die nicht Nullstellen im Zähler sind