UHU-Startseite►Mathematik►Jahrgangsstufen►11►Natürliche Exponential- und Logarithmusfunktion►Der natürliche Logarithmus►
Einige Grenzwerte


Grenzwerte I nach "Anschauliche Analysis 2":Baierlein, Barth, Greifenegger, Krumbacher
`lim_(x->oo)ln(x)/x`; Substitution: `x = e^u` mit `u->oo`
`=lim_(u->oo)(ln e^u)/e^u = lim_(u->oo)u/e^u = 0` und
`=> lim_(x->oo)x/ln x -> oo`


Grenzwerte II
Wächst die Wurzelfunktion stärker als der Logarithmus?
Vergleiche allgemein `x^r` mit `r in "IR"^"+"`:

`lim_(x->oo)ln(x)/x^r = lim_(u->oo) ln(e^(u/r))/(e^(u/r))^r = lim_(u->oo)(1/r*u)/e^u = 0`



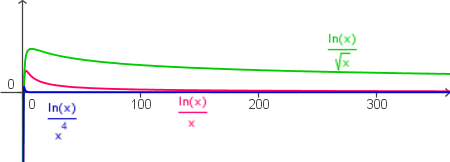
Wachstum ln

Wachstum der ln-Funktion
Der natürliche Logarithmus wächst schwächer als `x^r` (`r in "IR"^"+"`):
`lim_(x->oo)ln(x)/x^r = 0`   oder   `lim_(x->oo)x^r/ln(x) -> oo`
"Der Logarithmus verliert immer!"



Grenzwerte III
`lim_(x->0+0) x*ln(x)` Substitution: `x = 1/u` `lim_(u->oo) ln(1/u)/u = lim_(u->oo) -ln(u)/u = 0`

Noch besser:
`lim_(s->0+0) x^r*ln(x) = lim_(u->oo) (1/u^(1/r))^r*ln(u^(1/r)) = lim_(u->oo)(-r*ln(u)/u) = 0`


Wichtiger Grenzwert
`lim_(x->0+0) x^r*ln(x) = 0`




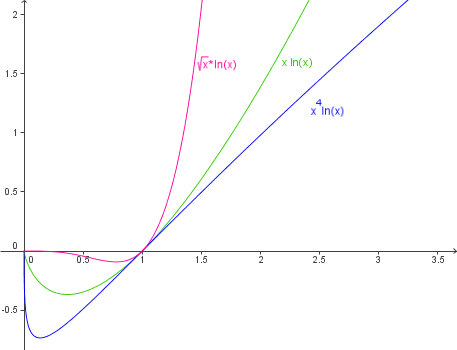
Produkt Potenzfunktion-ln(x)
optimal sichtbar mit Firefox Formeln mit asciimath Druckversion