Lokale Linearisierung von f(x)=x² bei xo=1
| Tangente im Punkt P(1|1) | nach "Analysis verständlich unterrichten":Danckwerts, Vogel |
Die Tangentengleichung in P(1|1) beträgt dann mit
`t(x) = f(x_o) + m(x-x_o)`
`t(x) = 1 + 2*(x-1)`
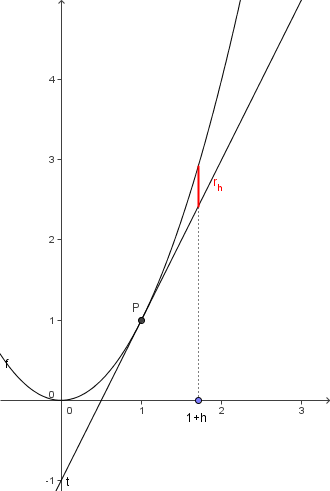
Abweichung r(h) an der Stelle 1+h
| Berechnung von r(h) für die Tangente | nach "Analysis verständlich unterrichten":Danckwerts, Vogel |
`= (1+h)^2 - (2h+1)`
`= 1^2 + 2h + h^2 - 2h - 1`
`= h^2`
also `lim_(h->0) r(h) = 0`
| Berechnung von r(h) für eine andere Gerade durch P | nach "Analysis verständlich unterrichten":Danckwerts, Vogel |
`r_1(h) = (1+h)^2 - (m_1(1+h-1)+1)`
`r_1(h) = 1 + 2h +h^2 - m_1*h -1`
`r_1(h) = h^2 + (2-m_1)*h`
also auch hier `lim_(h->0)r(h) = 0`
`r_h` strebt für jede Gerade durch P absolut gegen 0.
| Besonderheit der Tangente | nach "Analysis verständlich unterrichten":Danckwerts, Vogel |
für t(x) gilt `(r(h))/h = h => lim_(h->0) (r(h))/h = 0`
für g(x) gilt `(r_1(h))/h = h + (2-m_1) => lim_(h->0)(r_1(h))/h = (2-m_1) ne 0`
Nur für die Tangente wird auch der relative Fehler `(r(h))/h` 0, wenn h gegen 0 geht.