Vorüberlegungen
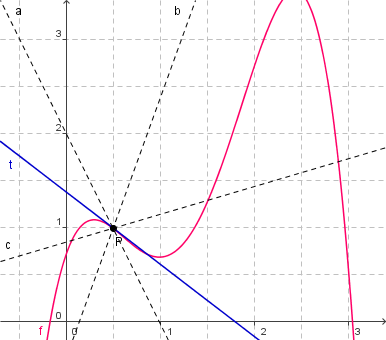
Geradenbüschel durch P
- t(x) scheint von allen Geraden diejenige zu sein, die f(x) um P herum am ehesten entspricht
- oder: t(x) approximiert f(x) lokal um P am besten.
| Geradenbüschel durch einen Punkt P |
- Wenn die Geraden durch den Ursprung gingen, dann wären der freie Parameter nur die Steigung: `g_m(x) = m*x`
- Der Ursprungspunkt ist aber um `1/2` nach rechts und `1` nach oben verschoben: `g_m(x) = m*(x-1/2)+1`
| Die Gerade t als besondere Gerade |
- Sie scheint dem Funktionsverlauf in P am "ähnlichsten" zu sein
- insbesondere ist das gut beim "Heranzoomen" erkennbar.
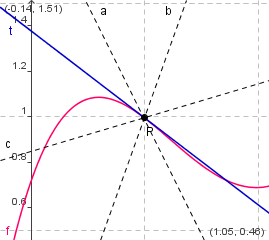
Geradenbüschel durch P, vergrößert
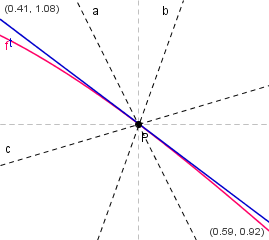
Geradenbüschel durch P, nochmal vergrößert
| Tangente an eine Funktion |
Die Tangente ist diejenige Gerade, die eine Funktion um einen Punkt P herum am besten approximiert.
Dies ist eine Erweiterung des geometrischen Tangentenbegriffes aus der Mittelstufe.