ln(x) zuerst
| Stammfunktion zu `x^-1` |
- Zu `int 1/x dx` existiert keine bisher bekannte Stammfunktion
- Existenz und Vermutungen über die Darstellung der Fläche unter dem Graphen von `f(x) = 1/x` :
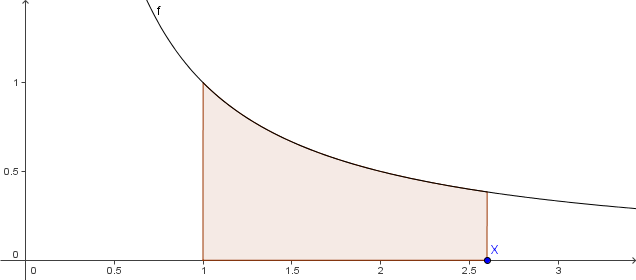
Unbestimmtes Integral über `x^-1`
- `D = RR^text(+)`
- `L'(x) = 1/x > 0 => L` ist stetig und streng monoton über `D`
- `L(1) = 0` also `x_o = 1` einzige Nullstelle, da L monoton steigend
- `=>`
- `x lt 1 => L(x) lt 0`
- `x = 1 => L(x) = 0`
- `x > 1 => L(x) > 0`
- Darstellung als Spur in Geogebra
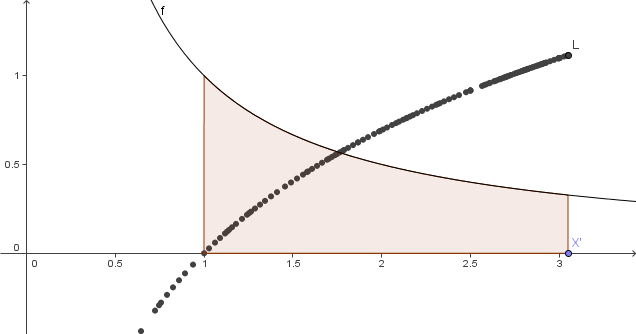
Darstellung von L(x)
| L(x) ist eine Logarithmusfunktion: L(ax)=L(a)+L(x) |
`z'(x) = 1/(ax)*a = 1/x = L'(x)`
`L(a*x)` ist also wie L(x) eine Stammfunktion von `L'(x)`
also gilt: `L(a*x) = L(x)+C`
`C = ?`
Wie schon gesehen, gilt `L(1) = 0`
Ausnutzen zur Bestimmung von C:
`L(a) = L(a*1) = L(1) + C = 0 + C = C`
also `L(a) = C`
`=> L(ax) = L(a) + L(x)`
| L(x) ist eine Logarithmusfunktion L(a/b) = L(a)-L(b) |
| L(x) ist eine Logarithmusfunktion L(a^r)=r L(a) |
-
`r in NN`:
`L(a^n) = L(a*a*...*a) = L(a) + L(a) + ... + L(a) = n*L(a)` -
`r in ZZ`:
`n in NN, L(a^-n) = L(1/a^n) = L(1) - L(a^n) = -n*L(a)` -
`r in QQ`:
`n in ZZ, L(a) = L((a^(1/n))^n) = n*L(a^(1/n)) => L(a^(1/n)) = 1/n*L(a)` -
`r in RR`:
Beweis mit Intervallschachtelung zwischen rationalen Exponenten, zu aufwändig für die Schule
| Alternative Argumentation über die Nullfunktion |
`ln(ax) = ln(a) + ln(x)`,
dann ist
`n_a(x) = ln(ax) - (ln(a)+ln(x))` die Nullfunktion.
Demzufolge muss `n_a'(x)` ebenfalls Nullfunktion sein:
`n_a'(x) = 1/(ax)*a - (0 + 1/x) = 1/x - 1/x = 0`
Damit ist nachgewiesen, dass deren Stammfunktion `n_a(x)` eine konstante Funktion ist. Jetzt muss noch gezeigt werden, dass sie immer 0 ist. Dazu setzt man den einzig bekannten Funktionswert ein:
`x = 1 => n_a(1) = ln(a) - (ln(a) + ln(1)) = 0`
`n_a(x)` ist also die Nullfunktion `=> ln(ax) = ln(a) + ln(x)`
`ln(x^a) = a*ln(x)` dann ist
`m_a(x) = ln(x^a) - a*ln(x) = 0` die Nullfunktion
`m_a'(x) = 1/(x^a)*a*x^(a-1) - a*1/x = a*1/x - a*1/x = 0`
Die Ableitung entspricht der Nullfunktion.
`m_a(x)` ist also eine konstante Funktion suche den Funktionswert für `x=1` und a beliebig:
`m_a(1) = ln(1^a) - a*ln(1) = 0 - a*0 = 0`, die konstante Funktion besitzt also überall den Wert 0:
`m_a(x) = 0 => ln(x^a) = a*ln(x)`