exp(x) zuerst, Bestimmung von `b^x`
| Zur Ableitung von `b^x` |
- Betrachte den Differenzenquotienten `(b^(x+h)-b^x)/h = (b^x*b^h-b^x)/h = b^x*(b^h-1)/h`.
- Gesucht ist also: `lim_(h->0) (b^h-1)/h`
- Untersuchung in einem Tabellenkalkulationssystem:
b h-> 0,10000 0,01000 0,00100 0,00010 0,00001 1,5 0,41380 0,40629 0,40555 0,40547 0,40547 2,0 0,71773 0,69556 0,69339 0,69317 0,69315 2,5 0,95958 0,92050 0,91671 0,91633 0,91629 3,0 1,16123 1,10467 1,09922 1,09867 1,09862 3,5 1,33462 1,26064 1,25355 1,25284 1,25277 4,0 1,48698 1,39595 1,38726 1,38639 1,38630
- Der Grenzwert a scheint zu existieren und ist von der Basis b abhängig.
- Die Ableitung einer Potenzfunktion `f(x) = b^x` ist wieder eine allgemeine Potenzfunktion `f'(x) = a*b^x` mit `a = lim_(h->0)(b^h-1)/h`
- Gibt es eine Exponentialfunktion, deren Ableitung exakt der Funktion selbst entspricht (Identität für das "Ableiten")?
- → Für welches b ergibt sich `lim_(h->0)(b^h-1)/h = 1`?
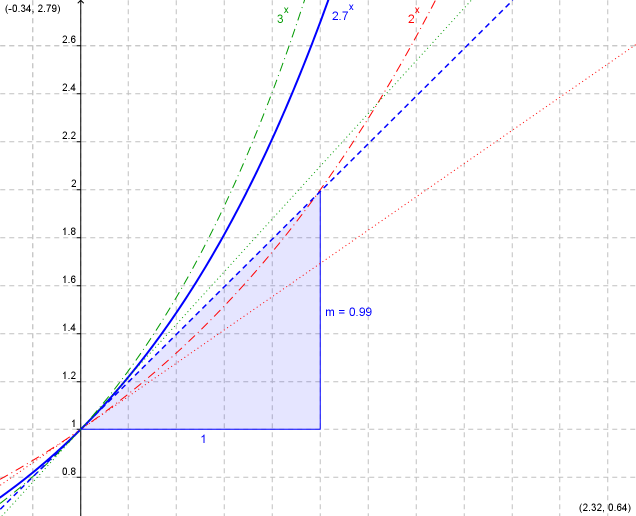
b^x mit drei verschiedenen Basen und der Steigung in x=0
| Auf der Suche nach f(x) = f'(x) |
-
Interpretation von `(b^h-1)/h = 1` als Ableitung von `f(x) = b^x` mit Steigung 1 im Punkt 0
⇒ Variation von b und Ausgabe der Steigung in geogebra:
-
Bestimmung einer Folge für die Basis über algebraische Umformungen
`lim_(h->0)(b^h-1)/h=1`
für kleine h: `(b^h-1)/h ~~ 1 => b^h ~~ 1+h`
oder `b ~~ (1+h)^(1/h)`
Substitution: `r = 1/h`
`b ~~ (1+1/r)^r` für sehr große r
Untersuchung mit Tabellenkalkukation:(vereinfachtes Beispiel) r 1 10 100 1000 10000 10000 100000 1000000 (1+1/r)^r 2,0000 2,5937 2,7048 2,7169 2,7181 2,7181 2,7183 2,7183
ergibt einen klaren Grenzwert mit b = 2,718281828 - Untersuchung der Steigungsfunktion verschiedener Exponentialfunktionen mit parametrisierter Basis:
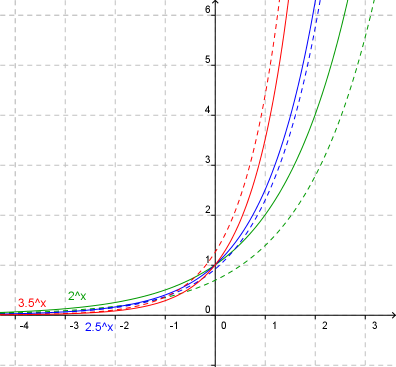
Verschiedene Exponentialfunktionen mit Ableitung
| Die natürliche Exponentialfunktion |
Verwendet man e = 2.7182818828... als Basis einer Exponentialfunktion `f(x) = e^x`, dann liegen die Tangentensteigungen am Graphen genau so, dass auch `f'(x) = e^x`.
Diese Exponentialfunktion heißt natürliche Exponentialfunktion, e nennt man die Euler'sche Zahl.
Diese Exponentialfunktion heißt natürliche Exponentialfunktion, e nennt man die Euler'sche Zahl.