Aspekte zur "klassischen" Tangentensteigung
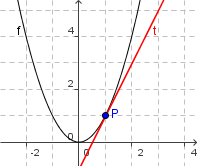
Tangente an Normalparabel
| Definition der Steigung eines Kurvenpunktes | nach "Analysis verständlich unterrichten":Danckwerts, Vogel |
- Die Steigung des Graphen in einem Punkt definiert sich über die Steigung der Gerade, die sich dem Graphen am besten anschmiegt.
- Diese Gerade wird Tangente an der Kurve genannt.
- Der Tangentenbegriff ist ursprünglich mit der Geometrie ("die Berührende") verbunden und muss analytisch erweitert werden.
- Beispiel: Waagerechte Tangente an die x³-Kurve im Nullpunkt.
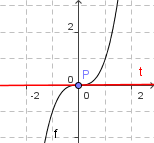
Tangente an x³: schneidet, statt zu berühren

Sekanten an Normalparabel
| Die Tangente als "Grenz"-Sekante | nach "Analysis verständlich unterrichten":Danckwerts, Vogel |
- Betrachtung einer einfachen gekrümmten Funktion (typischerweise f(x)=x²)
- Zur Findung der Tangente im Punkt P
- wird zunächst zusätzlich ein Punkt `Q in G_f` mit `x_P lt x_Q` definiert
- der mit Q zusammen eine "Sekante" von f(x) festlegt
- das Links-Wandern von Q entlang des Graphen definiert eine Folge von Sekanten
- die beim Übergang von Q nach P in der Tangente ihren Abschluss findet
- Die Sekante PQ darf nicht mit der Strecke [PQ] verwechselt werden (deren Länge sich auf 0 "zusammenziehen" würde
- Da diese Betrachtung die Umgebung miteinschließt, ist der hier verwendete Tangentenbegriff anders als
- die Definition der Tangente als die optimale Schmieggerade in P (dazu müsste diejenige Gerade durch P gesucht werden, die den Funktionsverlauf am genauesten wiedergibt)
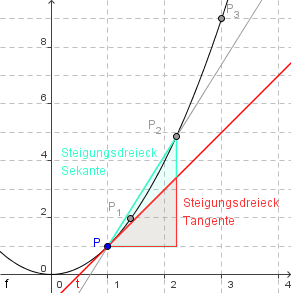
Steigungsdreiecke für Sekante und Tangente
| Berechnung der Tangentensteigung als Grenzwert | nach "Analysis verständlich unterrichten":Danckwerts, Vogel |
- Sekantensteigung: `m_s(x) = (f(x)-f(x_o))/(x-x_o)` (Differenzenquotient)
- Tangentensteigung: `m_t(x) = lim_(x->x_o)(f(x)-f(x_o))/(x-x_o) := f'(x)` (Differenzialquotient)
- Beispiel f(x) = x² bei P(2|4)
- Differenzenquotient: `m_s(x) = (f(x)-f(2))/(x-2) = (x^2-4)/(x-2) = x+2`
- Differenzialquotient: `m_t(x) = lim_(x->2)(f(x)-f(2))/(x-2) = 2+2 = 4`
- Zähler und Nenner des Differenzenquotienten gehen gegen Null, der Grenzwert ist trotzdem wohldefiniert
- Das Problem der Grenzwertbildung ist nur noch im algebraischen Kontext vorhanden