Eine Funktion mit `f'(x_o)>0`,dort aber nicht streng monoton steigend
| Definition der Funktion |
- `f(x) = {(x + 2x^2*sin(1/x), text(für) x!=0),(0, text(für) x=0):}`
- `f'(x) = 1 + 4*x*sin(1/x) - 2*cos(1/x) text( für ) x!=0` oszilliert umso schneller je näher bei 0 wg. `2*cos(1/x)`
-
Untersuchung von f'(0) mit Hilfe des Differentialquotienten:
`f'(0) = lim_(h->0)(f(x_o +h)-f(x_o))/h = lim_(h->0)(f(h)-f(0))/h = lim_(h->0)(h+2*h^2*sin(1/h)-0)/h`
Da `sin(x)` zwischen `-1` und `+1` schwankt gilt folgende Ungleichung:
`lim_(h->0)(h+2*h^2*(-1))/h le lim_(h->0)(f(h)-f(0))/h le lim_(h->0)(h+2*h^2*(+1))/h`
`lim_(h->0) 1-2h le lim_(h->0)(f(h)-f(0))/h le lim_(h->0) 1+2h`
`1 le lim_(h->0)(f(h)-f(0))/h le 1` also
`lim_(h->0)(f(h)-f(0))/h = 1`
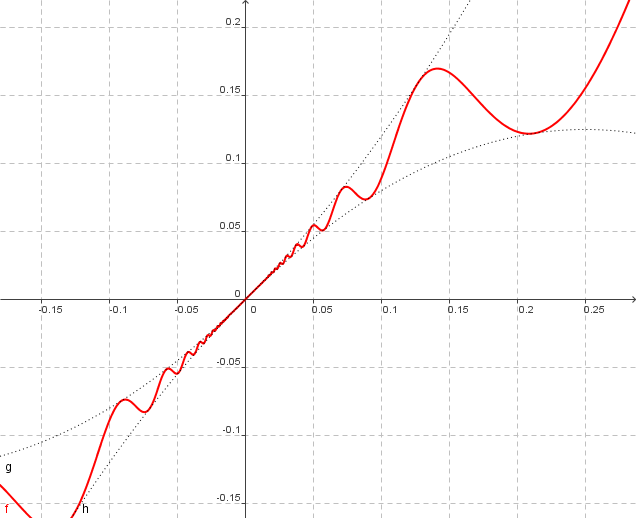
f'(0) > 0, dort nicht streng monoton