gegenseitige Lage von Geraden und Ebenen zueinander
| Ausgangssituation |
- `A(0|0|2); B(0|-2|2); C(0|2|0); vec u = ((-1),(0),(1)); vec v = ((0),(-1),(0)); vec w = ((-1),(0),(0));`
- `E_1: vec X = A + lambda*vec u + mu*vec v`
- `g_1: vec X = B + lambda*vec w`
- `g_2: vec X = C + lambda*vec u`
- `g_3: vec X = A + lambda*vec v`
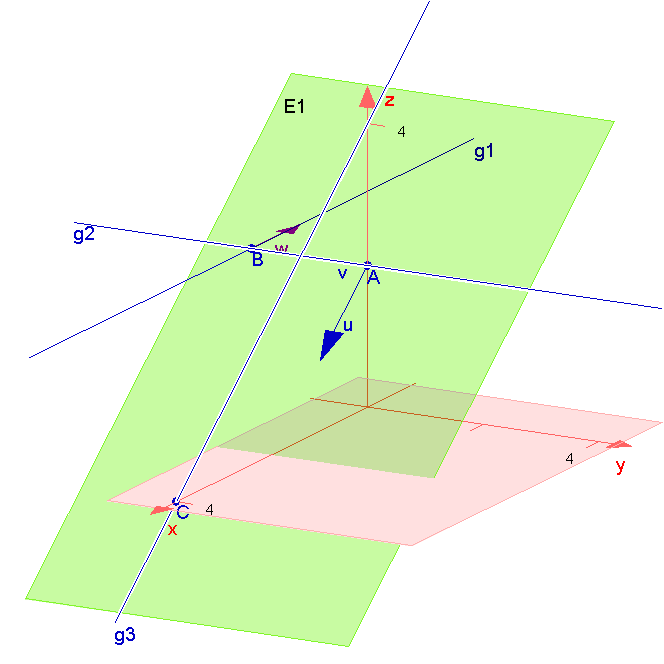
Verschiedene Geraden und eine Ebene
| Lage von E1 und g1 |
- Wie man sieht, treffen sich E1 und g1 genau in einem Punkt, die Gerade durchstößt die Ebene.
- Wie lässt sich dieser Punkt berechnen?
- Gleichsetzen von Gerade und Ebene ergibt drei Gleichungen mit drei Unbekannten.
- Einfacher: Einsetzen der Parameter
| Lagebeziehungen |
- `g in E` in der Ebene enthalten
- h || E parallel zur Ebene
- `j nn E != {}` schneidet die Ebene
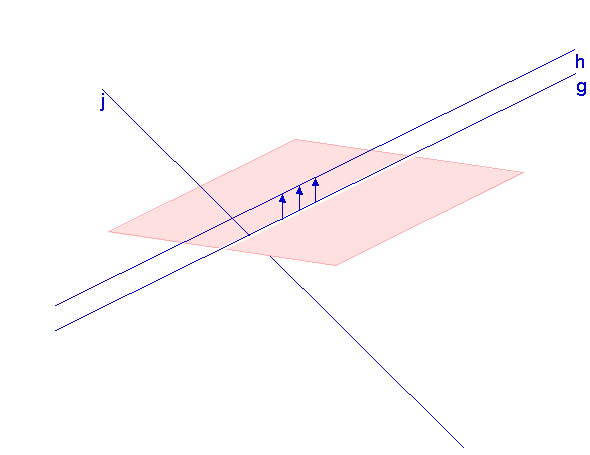
Lagebeziheungen von Geraden und Ebene