Extremwertaufgabe mit Wurzelfunktion

Maximaler Flächeninhalt bei gegebener Hypothenuse

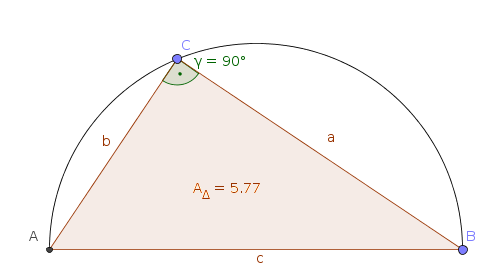
Von einem rechtwinkligen Dreieck ist die Hypothenuse mit der Länge c = 5cm gegeben. Wähle die Länge der Kathete a so, dass der Flächeninhalt des Dreiecks maximal wird.

Gegebene Hypothenuse

Flächenfunktion

`c = 5 = konst`

Pythagoras: `a^2 + b^2 = c^2`
Wähle x = a `=> b=sqrt(5^2-x^2)`
Flächeninhalt:`A(x)=1/2*x*b=1/2*x*sqrt(5^2-x^2)` mit $D_f = \mathbb{R}$

Extremwertbestimmung

Suche des Maximums über die Ableitung:
`f'(x) = (25 - 2·x^2)/(2·sqrt(25 - x^2))`
`f'(x) = 0 = (25 - 2·x^2)/(2·sqrt(25 - x^2))`
`=> 25 - 2x^2 = 0 => x_(1/2)=+-(5*sqrt 2)/2` negative Lösung ist nicht definiert
`x = (5 sqrt2)/2 ~~ 3.54`

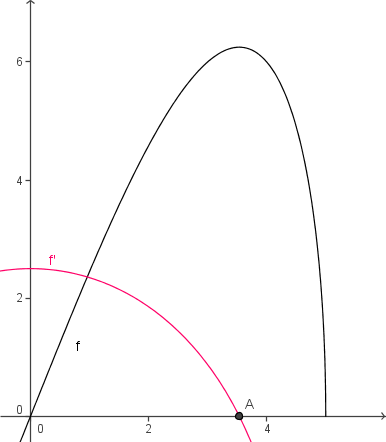
Extremwert gegebene Hypothenuse, Funktion

Interpretation des Ergebnisses

`a = (5*sqrt2)/2 => b = sqrt(25 - (25*2)/4) = sqrt(25/2) = (5 sqrt2)/2 = a`
a = b; es ergibt sich also ein gleichschenklig-rechtwinkliges Dreieck.
Die symmetrische Lösung ist also die mit dem maximalen Flächeninhalt.