Ableitungsfunktion


Definition
Die Ableitungsfunktion f'(x) einer Funktion f(x) ist diejenige Funktion, die jedem x den Wert der Tangentensteigung an Gf zuordnet:

`f: x|->f(x)`
`f': x|->text(Steigung der Tangente an) G_f`

(Geht natürlich nur dort, wo sich eindeutige Tangenten an die Funktion anlegen lassen)



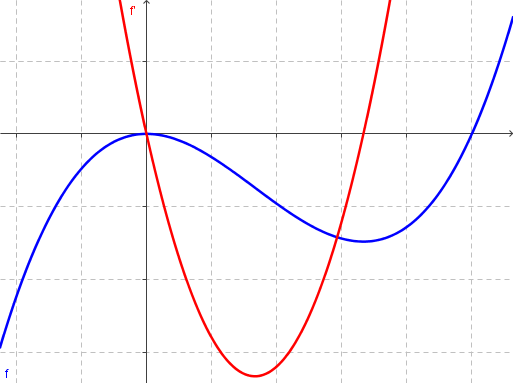
Funktion f mit Ableitungsfunktion f'

Beispiel für eine Ableitungsfunktion
`f(x) = -5x^2`
`f'(x) = lim_(h->0) (f(x+h)-f(x))/h = lim_(h->0) (-5(x+h)^2+5x^2)/h`
` = lim_(h->0) (-5*(x^2+2xh+h^2)+5x^2)/h = lim_(h->0)(-10xh-h^2)/h = lim_(h->0) -10x - h = -10x`
`f'(x) = -10x`
`f'(1) = -10` (Momentangeschwindigkeit nach 1 Sekunde)
`f'(0) = 0`
`f'(2) = -20` (Momentangeschwindigkeit nach 2 Sekunden)




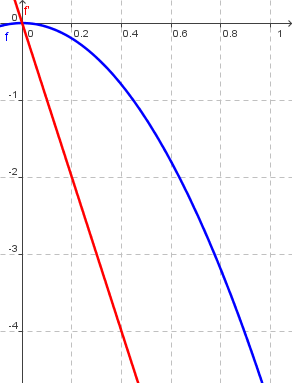
Beispiel für eine Ableitungsfunktion