Begriff der Differenzierbarkeit, Abgrenzung insbesondere durch die Betragsfunktion
| Die Betragsfunktion |
- Fallunterscheidung, je nachdem ob die Zahl größer oder kleiner als Null ist
- Es handelt sich also um zwei Funktionsterme, die je nach x-Wert angewendet werden
- Die Funktion ist aus zwei verschiedenen Funktionen zusammengesetzt
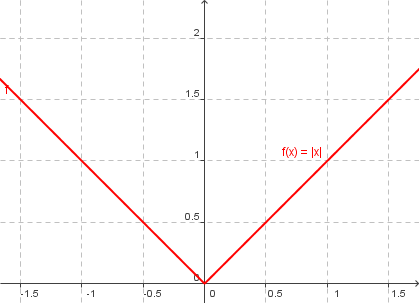
Die Betragsfunktion
| Tangentensteigung für die Teilfunktionen |
`(f(x_0+h)-f(x_0))/h = (x_0+h-x_0)/h = h/h = 1`
Die Tangentensteigung beträgt in jedem Punkt +1
2. Fall `x lt 0`
`(f(x_0+h)-f(x_0))/h = (-x_0-h+x_0)/h = (-h)/h = -1`
Die Tangentensteigung beträgt in jedem Punkt -1
Zusammenfassung:
`f'(x_0)={(+1,text(für ) x>=0),(-1,text(für ) x lt 0):}`
| Untersuchung von x = 0 |
`lim_(h->0) (f(x_0+h)-f(x_0))/h = -1` wenn `h lt 0`
Eine Tangentensteigung kann nicht bestimmt werden!
| Differenzierbarkeit |
Eine Funktion f(x) heißt an einer Stelle `x_0` differenzierbar, wenn
`lim_(h->0) (f(x_0+h)-f(x_0))/h` so existiert,
dass sich für positives und negatives h der gleiche Wert ergibt.
`lim_(h->0) (f(x_0+h)-f(x_0))/h` so existiert,
dass sich für positives und negatives h der gleiche Wert ergibt.
- einen KNICK, noch
- einen SPRUNG