|
Die Logarithumsfunktion als Umkehrfunktion zur Exponentialfunktion
| Eigenschaften der Exponentialfunktion |
Die Exponentialfunktion `x|->a^x, x in RR` ordnet zu:
| Exponent | `|->` | Potenzwert |
| Beispiel: |
| `x` | `|->` | `2^x` |
| -2 | | 0,25 |
| -1 | | 0,5 |
| -0 | | 1 |
| +1 | | 2 |
| +2 | | 4 |
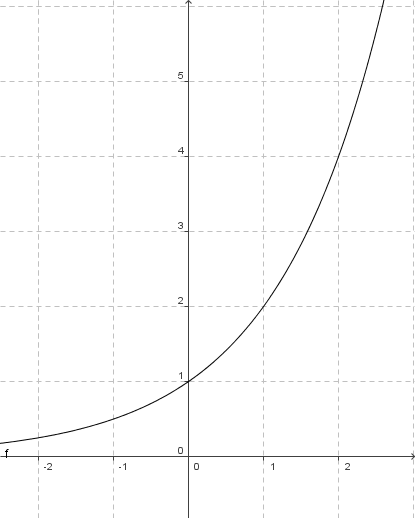
Die Exponentialfunktion 2<sup>x</sup>
- alle Funktionswerte sind größer als Null: `a^x > 0, x in RR`
- jeder Funktionswert wird genau einmal angenommen, die Funktion ist sogar monoton steigend oder streng monoton fallend: `f(x_1)` < `f(x_2)` für `x_1` < `x_2` oder `f(x_1)` > `f(x_2)` für `x_1` < `x_2`
ordnet zu `x |-> log_a(x), x in RR^text(+)`
| Potenzwert | `|->` | Exponent |
| im Beispiel: |
| `x` | `|->` | `log_2(x)` |
| 0,25 | | -2 |
| 0,5 | | -1 |
| 1 | | 0 |
| 2 | | +1 |
| 4 | | +2 |

Logarithmus von x zur Basis 2
- nur für positive x definiert: `D = RR^"+"`
- Nullstelle bei x = 1: `log_a(1) = 0`
- `log_a(a) = 1` und `log_2(1/a) = -1`
| Definition der Logarithmusfunktion |
Die Logarithmusfunktion `log_a(x)`
- ordnet einem Potenzwert x den passenden Exponenten (zur Basis a) zu
- gibt den Exponenten y von a aus für den gilt `a^y = x`
- beantwortet die Frage "a hoch wieviel ist x?"
|

