Interpretation geometrischer Größen in t-a, t-v und t-x - Diagrammen

Steigungen im t-x-Diagramm

Eine Steigung im t-x-Diagramm entspricht immer einem Quotienten Δx   =  v Δt
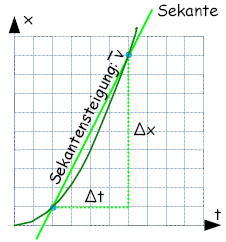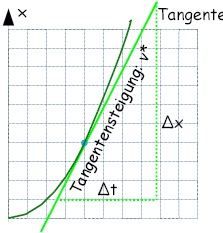Mit der Sekantensteigung erhält man die mittlere Geschwindigkeit zwischen zwei Punkten	Mit der Tangentensteigung erhält man die Momentangeschwindigkeit in einem Punkt

Steigungen im t-v-Diagramm

Eine Steigung im t-v-Diagramm entspricht immer einem Quotienten Δv   =  a Δt
Sekantensteigungen ergeben mittlere Beschleunigungen,	Tangentensteigungen Momentanbeschleunigungen.

Flächen im t-a-Diagramm

Eine Fläche im t-a-Diagramm entspricht immer dem Produkt a(t)·Δt = Δv
Mit der Fläche unterhalb des Graphen erhält man die Geschwindigkeitsänderung in diesem Zeitintervall.
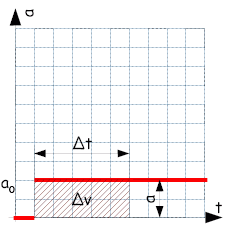	Im Beispiel: Δv = a0·Δt

Flächen im t-v-Diagramm

Eine Fläche im t-v-Diagramm entspricht immer dem Produkt v(t)·Δt = Δx
Mit der Fläche unterhalb des Graphen erhält man die Ortsänderung in diesem Zeitintervall.
	Im Beispiel: Δx = 1 v(t)·Δt 2

Zusammenfassung

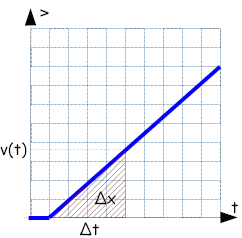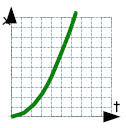
Ortsfunktion x(t)
⇓ Tangentensteigung ⇓	⇑ Fläche unter der Funktion ⇑
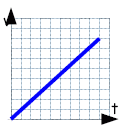
Geschwindigkeitsfunktion v(t)
⇓ Tangentensteigung ⇓	⇑ Fläche unter der Funktion ⇑
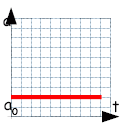
Beschleunigungsfunktion a(t)