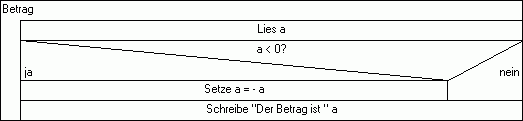
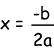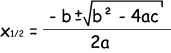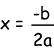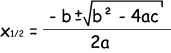Zuerst ein einfacher Fall: Die Betragsfunktion. Sie bestimmt den Abstand einer Zahl vom Ursprung der Zahlengerade.
betrag( -679201 ) = +679201
betrag( -5 ) = +5
betrag( -2 ) = +2
betrag( 0 ) = 0
betrag( +12394 ) = +12394
Wie man sieht, bleiben positive Zahlen und die 0 unverändert, negative Zahlen werden positiv.
Eine Entscheidung kann anhand der Position der Zahl auf der Zahlengerade herbeigeführt werden.
Ist die Position:
- <0, dann muss das Vorzeichen der Zahl umgedreht werden
- sonst bleibt die Zahl wie sie ist
Je nach dem Zahlenwert muss also etwas anderes passieren, andere Anweisungsfolgen müssen ausgeführt werden. Im Struktogramm wird die Verzweigung durch eine Frage und ein Aufspalten des Konrtollflusses dargestellt:
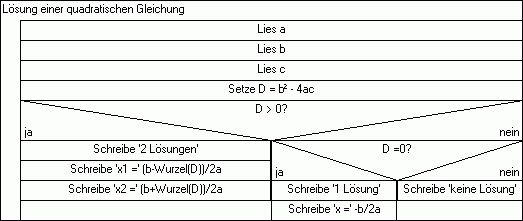
Untersuchen wir den Vorgang zur Berechnung der Lösung einer quadratischen Gleichung
ax2+bx+c = 0
Die Gleichung kann z.B. so gedeutet werden, dass nach den Schnittpunkten einer Parabel mit der x-Achse gesucht wird.
Um diese zu bestimmen, ist es günstig zu wissen wieviele Lösungen es gibt.
Dazu bestimmt man zuerst den Wert der Diskrimante:
b²-4ac
Ist sie
- <0, dann gibt es keine Lösung
- =0, dann gibt es genau eine Lösung:
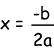
- >0, dann gibt es zwei Lösungen:
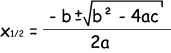
Ein Programm zur Lösung der quadratischen Gleichung erwartet also als Eingabe die Parameter a, b und c (Koeffizienten) und gibt anschließend die Lösungsmenge aus.
Das Javaprogramm unter Verwendung des Paketes myio:
package myprojects.auswahl;
import myio.*;
import java.lang.Math.*;
class Auswahl {
public static void main(String args[]) {
InOut.writeln( "Bitte a eingeben: " );
double a = InOut.readDouble();
InOut.writeln( "Bitte b eingeben: " );
double b = InOut.readDouble();
InOut.writeln( "Bitte c eingeben: " );
double c = InOut.readDouble();
double D = b*b - 4*a*c;
InOut.writeln( "Diskriminante: "+D );
if (D > 0) {
InOut.writeln( "Zwei Lösungen: ");
double x1 = (-b - Math.sqrt( D ))/(2*a);
double x2 = (-b + Math.sqrt( D ))/(2*a);
InOut.writeln( "L = {"+x1+"; "+x2+"}" );
} else {
if (D == 0) {
double x = -b/(2*a);
InOut.writeln( "Es gibt eine Lösung: L = {"+b+"}" );
} else {
InOut.writeln( "Es gibt keine Lösung: L = {}" );
}
}
}
}
Der Quelltext im einzelnen:
InOut.writeln( "Bitte a eingeben: " );
double a = InOut.readDouble();
InOut.writeln( "Bitte b eingeben: " );
double b = InOut.readDouble();
InOut.writeln( "Bitte c eingeben: " );
double c = InOut.readDouble();
Eingabe der Koeffizienten a, b und c. Hierbei werden die reellen Zahlen mit sogenannter "doppelter Genauigkeit" gespeichert ("double").
double D = b*b - 4*a*c;
InOut.writeln( "Diskriminante: "+D );
Berechnung der Diskrimante D und Ausgabe ihres Wertes.
if (D > 0) {
InOut.writeln( "Zwei Lösungen: ");
double x1 = (-b - Math.sqrt( D ))/(2*a);
double x2 = (-b + Math.sqrt( D ))/(2*a);
InOut.writeln( "L = {"+x1+"; "+x2+"}" );
} else {
Verzweigung in den Fall mit zwei Lösungen. Hier werden x1 und x2 berechnet und anschließend in einer Lösungsmenge ausgegeben.
} else {
if (D == 0) {
double x = -b/(2*a);
InOut.writeln( "Es gibt eine Lösung: L = {"+b+"}" );
} else {
InOut.writeln( "Es gibt keine Lösung: L = {}" );
}
}
Verzweigung in die anderen Fälle. Für D=0 wird die eine Lösung berechnet, für D < 0 wird die leere Menge als Lösung ausgegeben.
Eine Auswahl besteht immer aus einem "if" in Verbindung mit einer "Bedingung" und ein oder zwei Anweisungsblöcken:
Einseitige Auswahl: Die Anweisungen im if-Block werden nur ausgeführt, wenn die Bedingung erfüllt ist.

if (<Bedingung>) {
<Anweisungsblock für erfüllte Bedingung>
}
Zweiseitige Auswahl: Bei erfüllter Bedingung werden die Anweisungen des ersten Bocks ausgeführt, alternativ werden die Anweisungen des 2. Blocks ausgeführt.

if (<Bedingung>) {
<Anweisungsblock für erfüllte Bedingung>
} else {
<Anweisungsblock, der ausgeführt wird, wenn die Bedingung nicht erfüllt ist>
}
Bedingungen sind wiederum logische Ausdrücke, sie können nur den Wert wahr oder falsch annehmen.
Logische Ausdrücke wiederum setzen sich aus Aussagen, sogenannten logischen "Atomen" und logischen Operatoren zusammen. Die gesamte Struktur einer Verzweigung ist hier noch einmal dargestellt:

Beispiele:
if (a < 0) a = -a;
if (x < 0) && (y < 1) a = x;
else a = y;
Aussagen sind Logische Atome, die als wahr oder falsch angesehen werden können. Beispiele:
"Heute hat es geregnet."
"Informatik ist ein Grundkursfach."
"In der Schule herrscht Anwesenheitspflicht."
"6 ist eine Primzahl."
"15 ist durch 5 teilbar: 5 | 15"
Man kann eine logische Aussage als eine Funktion ansehen:
f: (Deutscher Satz) -> (falsch;wahr)
Besonders gut eignen sich Aussagen aus der Mathematik, da nicht über deren Interpretation geredet werden muss.
Aussagen lassen sich durch logische Operatoren verbinden:
"Heute hat es nicht geregnet."
"Informatik ist nicht ein Grundkursfach."
"In der Schule herrscht nicht Anwesenheitspflicht."
"6 ist nicht eine Primzahl."
"15 ist nicht durch 5 teilbar."
Der NICHT-Operator invertiert das Ergebnis einer Aussage: aus "wahr" wird "falsch" und umgekehrt.
"Informatik ist ein Grundkursfach." und "In der Schule herrscht Anwesenheitspflicht."
"6 ist eine Primzahl." und "5 | 15"
Der UND-Operator verbindet zwei logische Aussagen zu einer neuen. Dabei gilt folgende Wahrheitstabelle:
| A1 |
A2 |
A1und A2 |
| falsch |
falsch |
falsch |
| falsch |
wahr |
falsch |
| wahr |
falsch |
falsch |
| wahr |
wahr |
wahr |
Der durch UND entstandene Ausdruck ist also nur dann wahr, wenn beide Teilaussagen wahr sind.
"Informatik ist ein Grundkursfach." oder "In der Schule herrscht Anwesenheitspflicht."
"6 ist eine Primzahl." oder "5 | 15"
Der ODER-Operator verbindet zwei logische Aussagen zu einer neuen. Dabei gilt folgende Wahrheitstabelle:
| A1 |
A2 |
A1oder A2 |
| falsch |
falsch |
falsch |
| falsch |
wahr |
wahr |
| wahr |
falsch |
wahr |
| wahr |
wahr |
wahr |
Der durch ODER entstandene Ausdruck ist also nur dann falsch, wenn beide Teilaussagen falsch sind.
Verbindet man verschiedene Aussagen über logische Operatoren so erhält man komplexere logische Ausdrücke. Beispiele:
1) a ODER b UND c UND NICHT d
2) a UND b ODER NICHT c UND NICHT d
Hier stellt sich die Frage, welcher Operator Vorrang hat (wie etwa "Punkt vor Strich" in der Zahlearithmetik), wie man logische Ausdrücke vereinfachen kann und wann sie äquivalent sind.
In der boolschen Algebra gilt NICHT vor UND vor ODER.
Im ersten Beispiel gilt also für die Belegung a=FALSE, b=FALSE, c=TRUE und d=TRUE:
FALSE ODER FALSE UND TRUE UND NICHT TRUE
FALSE ODER FALSE UND TRUE UND FALSE
FALSE ODER FALSE UND FALSE
FALSE ODER FALSE
FALSE
Um einen boolschen Term komplett zu erfassen ist es hilfreich seine Wahrheitstabelle aufzuschreiben:
| a | b | c | d | a ODER b UND c UND NICHT d |
| false | false | false | false | false |
| false | false | false | true | false |
| false | false | true | false | false |
| false | false | true | true | false |
| false | true | false | false | false |
| false | true | false | true | false |
| false | true | true | false | true |
| false | true | true | true | false |
| true | false | false | false | true |
| true | false | false | true | true |
| true | false | true | false | true |
| true | false | true | true | true |
| true | true | false | false | true |
| true | true | false | true | true |
| true | true | true | false | true |
| true | true | true | true | true |
Java hat mehrere Möglichkeiten Zahlenausdrücke in eine Aussage abzubilden. Dies findet im allgemeinen mit den Zahlenvergleichsoperatoren statt:
| Operator | Bedeutung | Beispiel |
| == | gleich | x == 3 |
| != | ungleich | x != 3 |
| < | kleiner als | x < 3 |
| > | größer als | x > 3 |
| <= | kleiner oder gleich | x <= 3 |
| >= | größer oder gleich | x >= 3 |
Um boolsche Zahlenausdrücke (Aussagen) zu verarbeiten gibt es die entsprechenden Operatoren natürlich auch in Java:
| Operator | Bedeutung | Beispiel |
| && | logisches Und | true && false |
| || | logisches Oder | true || false |
| ! | logische Negation | !true |
Beispiele:
Alle Zahlen, die sich im Koordinatensystem innerhalb des Einheitsquadrates befinden:

(-1 <= x) && (x <= +1) && (-1 <= y) && (y <= +1)
oder diese Punktmenge:
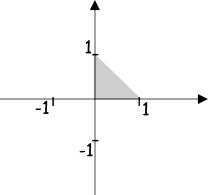
(0 <= x) && (x <= +1) && (0 <= y) && (y <= 1-x)
Ganzzahlen werden im Speicher des Computers auf einzelne Bits abgebildet. Eine typische Schreibweise ist die Verwendung von "L" für ein gesetztes und "O" für ein nicht-gesetztes Bit.
Beispiele bei Verwendung eines Bytes:
1 = OOOOOOOL
20 = OOOLOLOO
127 = OLLLLLLL
Die Codierung der Dezimalzahl erfolgt in der Reihenfolge, in der man ein Zahlenschloss mit jeweils nur zwei Möglichkeiten durchzählen würde:
OOOOOOOO 0
OOOOOOOL 1
OOOOOOLO 2
OOOOOOLL 3
OOOOOLOO 4
OOOOOLOL 5
OOOOOLLO 6
OOOOOLLL 7
OOOOLOOO 8
...
Da die einzelnen Bits unter Umständen für die Programmierung von Peripheriegeräten interessant sind, oder als Zustände für Prozessorvorgänge verwendet werden, gibt es eigene Operatoren, die mit dieser Bitdarstellung arbeiten:
| Operator | Bedeutung | Beispiel | Dualdarstellung | Ergebnis |
| & | Bitweises Und | 3 & 6 | 000000LL & 00000LL0 | 000000L0 |
| | | Bitweises Oder | 3 | 6 | 000000LL | 00000LL0 | 00000LLL |
| ^ | Bitweises X-Oder | 3 ^ 6 | 000000LL ^ 00000LL0 | 00000L00 |
| << | Linksverschiebung | 3 << 6 | 000000LL << 6 | LLOOOOOO |
Die X-Oder-Verknüpfung a ^ b invertiert dort in a das Bit, wo es in b gesetzt ist.
In den 80er Jahren wurden große Hoffnung in die AI (artificial intelligence, künstliche Intelligenz) gesteckt. Die Idee war, den Computer als "Experten" oder "Assistenten" bei speziellen Problemen zur Lösung heranziehen zu können.
Ein Ergebnis waren die "Assistenten" in den Office-Anwendungen oder im Betriebssystem "Windows".
Diese einfachen Vertreter der künstlichen Intelligenz arbeiten im einfachsten Fall mit Verzweigungen in einem Binärbaum, wie unten dargestellt:
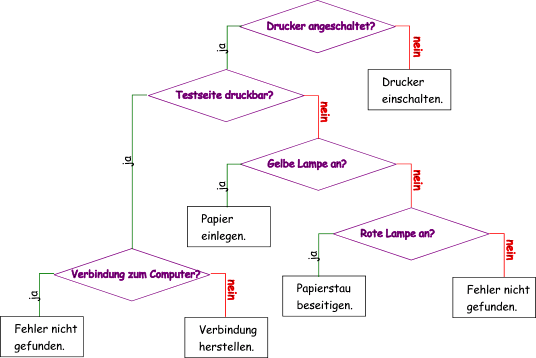
import myio.*;
class BinaryTreeExpert{
public static void main(String args[]){
String s;
InOut.writeln( "Ist der Drucker angeschaltet ? (j|n)" );
s = InOut.readString();
if (s.charAt(0) == 'j' || s.charAt(0) == 'J'){
InOut.writeln( "Ist eine Testseite vom Drucker aus druckbar?" );
s = InOut.readString();
if (s.charAt(0) == 'j' || s.charAt(0) == 'J'){
InOut.writeln( "Ist der Crucker mit dem Computer verkabelt?" );
s = InOut.readString();
if (s.charAt(0) == 'j' || s.charAt(0) == 'J'){
InOut.writeln( "Der Assistent kann den Fehler nicht finden." );
} else {
InOut.writeln( "Verbinden Sie den Computer und den Drucker mit einem geeigneten Kabel" );
}
} else {
InOut.writeln( "Leuchtet die gelbe Lampe am Drucker?" );
s = InOut.readString();
if (s.charAt(0) == 'j' || s.charAt(0) == 'J'){
InOut.writeln( "Legen Sie Papier in den Drucker ein." );
} else {
InOut.writeln( "Leuchtet die rote Lampe am Drucker?" );
s = InOut.readString();
if (s.charAt(0) == 'j' || s.charAt(0) == 'J'){
InOut.writeln( "Entfernen Sie den Papierstau." );
} else {
InOut.writeln( "Der Assistent kann den Fehler nicht finden." );
}
}
}
} else {
InOut.writeln( "Schalten Sie den Drucker ein." );
}
}
}
- Schreiben Sie ein Programm, das die Signumfunktion einer ganzen Zahl ausgeben kann.
- Schreiben Sie ein Programm, das die Lösung der Gleichung ax + b = c ausgeben kann. Berücksichtigen Sie dabei die Fallunterscheidung für a = 0.
- Erklären Sie die Funktion des folgenden Programms:

- Überprüfen Sie die folgenden logischen Ausdrücke auf Äquivalenz mit Hilfe einer Wahrheitstabelle:
a & (b | c) mit a | (b & c)(!a & !b) mit !(a | b)
- Wandeln Sie die folgenden Zahlen in einen Zahlenausdruck, der in einer Java-Verzweigung verwendet werden kann:
- Gesucht sind alle Koordinaten, deren x-Wert kleiner als 3 und deren y-Wert zwischen 7 und 7,1 liegt.
- Gesucht sind alle Koordinaten, deren x-Wert größer als das dreifache des y-Wertes ist.
- Bringen sie die folgenden Dezimalzahlen in ihre Dualdarstellung: 19, 32, 65, 126, 513
- Welches Ergebnis bekommen Sie bei folgenden Bitoperationen? 19 & 32; 19 & 65; 126 | 1;
- Stellen Sie die folgenden Punktmengen als Aussagen für x und y in Java dar.

- Zeichnen Sie einen binären Entscheidungsbaum für einen nicht-funktionierenden Videorekorder.
- Schreiben Sie ein kleines Smalltalk-Programm, welches auf Stichworte in einem eingegebenen Satz reagiert. Dazu muss die eingegebene Zeile nach einem bestimmten Wort durchsucht werden. Verwenden Sie dazu die Methode indexOf( < wort > ) der Klasse string