Modelle
Heinrich Hertz (Ende 19. Jahrhundert)
"Wir machen uns innere Scheinbilder oder Symbole der äußeren Gegenstände, und zwar machen wir sie von solcher Art, dass die denknotwendigen Folgen der Bilder stets wieder Bilder seien von den Folgen der abgebildeten Gegenstände."
Prinzip der Modellbildung
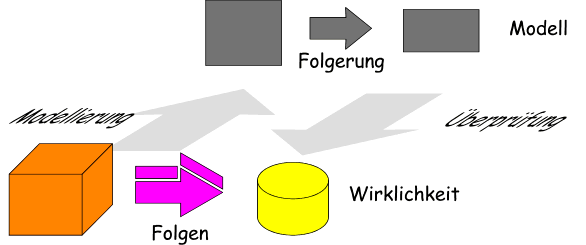
Der beobachtete Sachverhalt kann durch ein Modell nicht in seiner Gesamtheit erfasst werden. Dies wird in der Zeichnung durch eine "Projektion" angedeutet: Es findet ein Verlust an Information statt, das "Bild" des Sachverhalts ist nur noch zweidimensional.
Deshalb wird ein Projekt unter einem bestimmten "Aspekt" erstellt, es ist dann umso "brauchbarer" je eher sich der tatsächliche Sachverhalt mit dem Modell simulieren lässt.
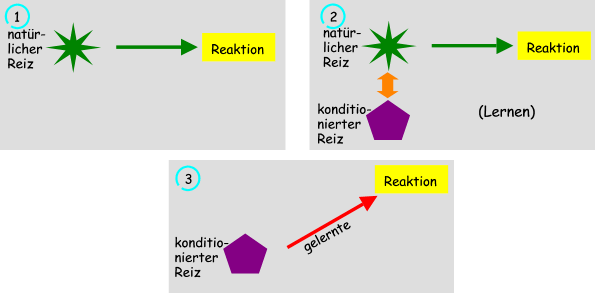
Reiz- Reaktionsreflex (Psychologie)
Der russische Psychologe Iwan Petrowitsch Pawlow erhielt 1904 für seine Untersuchung des Speichelflussreflexes bei Hunden den Nobelpreis.
Normalerweise müsste bei einem Hund der Speichelfluss ausgelöst werden, wenn er Kontakt mit der Nahrung aufgenommen hat. Pawlow konnte aber nachweisen, dass der Speichelfluss des Hundes bei regelmäßiger Fütterung bereits mit Erscheinen des Wärters stattfand.
In weiteren Versuchen konnte er sogar den Speichelfluss durch unterschiedliche Reize, wie zum Beispiel dem Ertönen einer Klingel auslösen.
Daraus leitete er das folgende "Lernmodell" ab (Reiz-Reaktions-Lernen oder klassisches Konditionieren).
Schema des Reiz-Reaktionslernens
Das Modell vom Massenpunkt (Physik)
In der Physik der 11. Klasse (Mechanik) werden verschiedene Bewegungen beschrieben: Horizontaler und schiefer Wurf, Kreisbewegung, Bewegungen bei linearem Kraftgesetz usw. Die Beschreibung erfolgt durch Angabe von x- und y- Koordinate des Körpers in der Zeit.
Aber werfen Sie einmal einen Bumerang. Wo (am Bumerang) befindet sich diese x- und y- Koordinate?
Wurf eines Bumerangs

Die Antwort scheint klar: Die (berechnete) Wurfparabel beschreibt die Bahn des Schwerpunkts. Ist dann der Wurf auf diese Weise vollständig beschrieben?
Angenommen der Bumerang fliegt nah einem Baum vorbei (dessen x- und y- Koordinaten auch bekannt sind). Wann wird der Baum getroffen?
Oder betrachten wir die für die "Rückkehr" so wichtige Drehung des Wurfgeschosses: Wird sie bei der Bahnbeschreibung mitberücksichtigt?
All diese Fragen entstehen, weil man dem Modell von der Bahnbeschreibung zuviel zumutet; es handelt sich lediglich um die Beschreibung der Bewegung eines Massenpunktes, in dem man sich die gesamte Masse des Objektes konzentriert denkt.
Ein typisches Problem bei der Modellierung ist die Verwechslung des Modells mit der Wirklichkeit. Das kann zu scheinbaren Paradoxien führen.
Zylinderparadoxon
In der Physik lässt sich das Verhalten von Elektronen unter bestimmten Bedingungen mit dem Verhalten eines "Teilchens" erklären, unter bestimmten Bedingungen aber nur mit dem Verhalten einer "Welle". Vergisst man, dass man sich nur ein Modell vom Elektron gemacht hat, so widerspricht sich dieses Verhalten:

Erst mit der Existenz des Elektrons als "Quantenobjekt" (das sich der bildhaften Vorstellung entzieht) lässt sich dieser scheinbare Widerspruch aufklären.
Achilles und die Schildkröte
Achilles und die Schildkröte laufen um die Wette. Da Achilles schneller ist, gibt er der Schildkröte einen Vorsprung.
Wettlauf

Betrachten wir den Lauf aus folgender Sicht:
In der Zeit, in der Achilles den Vorsprung der Schildkröte gelaufen ist, hat die Schildkröte selbst einen bestimmten Weg zurückgelegt; jetzt befindet sich Achilles an ihrer alten Position, die Schildkröte hat aber nach wie vor wieder einen Vorsprung. Ab hier lässt sich dieses Spiel unendlich oft wiederholen.
Also wird Achilles die Schildkröte niemals einholen!
Welcher Fehler wurde hier bei der Modellbildung gemacht? Der Ansatz ist vollkommen in Ordnung, nur spielt uns hier unsere Erfahrung einen Streich. Achilles holt die Schildkröte ein, wenn sich der Vorgang unendlich oft wiederholt hat, das ist aber trotzdem ein endliches Zeitintervall.
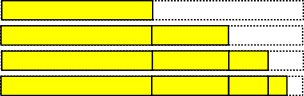
Beispiel: Wenn man zu einer Zahl unendlich oft die Hälfte und die Hälfte ihrer Hälfte, usw addiert, so erhält man (nach unendlichem Wiederholen) nur das Doppelte:
Unendliche Summe mit endlichem Ergebnis
Zusammenfassung
Es ist also immer zu testen, ob Erfahrungseindrücke und Assoziatonen, die mit der Modellbildung verbunden sind, den Modellannahmen widersprechen, oder ihnen gerecht werden.
Oder mit den Worten aus einem Physikbuch:
"Modelle sind also Vorstellungshilfen und Wirklichkeitshilfen, nicht die Wirklichkeit selbst." (Metzler Physik).
Daten in einem Datenbanksystem
beschreiben Objekte und Beziehungen zwischen ihnen, sie sind also ein "Bild" einer
Situation der Welt.
Dieses "Bild" wird erstellt um eine bestimmte Aufgabe zu bearbeiten. Nicht interessierende
Elemente werden dafür vernachlässigt.
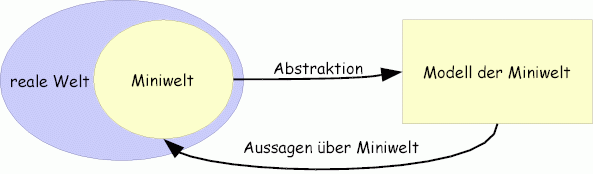
- Durch Betrachtung von Merkmalen, die für das Projekt wichtig sind wird
eine Teilmenge der tatsächlichen Objekte und Beziehungen erstellt (Miniwelt).
- Die in Frage kommenden Elemente der Miniwelt werden im Computer in ein
abstraktes System überführt. Hier werden Aufgaben bearbeitet und Aussagen
erstellt. Die Ergebnisse
müssen mit der Miniwelt und der realen Welt abgeglichen werden.






