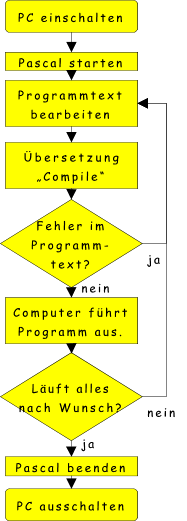
- Der Arbeitsprozess
- Struktur eines PASCAL-Programms
- Ein- und Ausgabe
- Beispiel: Programm zur Multiplikation zweier Zahlen
- Beispiel: Programm zur Berechnung linearer Gleichungen
- Rechenausdrücke in PASCAL
- Berechnungen zum regelmäßigen Vieleck
- Prinzip der Datenverarbeitung
| Struktur |
Syntax |
Kommentar |
| Programmkopf |
program example;
uses crt;
|
Hinter dem Stichwort "program" muss ein Bezeichner für das Programm stehen. |
Deklarations-
(Vereinbarungs-)
teil |
var
x: real;
i: integer;
|
Hier werden die Variablen (Speicherplatz) für das Programm vereinbart.
x: reelle Zahl; i: ganze Zahl.
|
| Anweisungsteil |
begin
readln( x );
for i := 1 to 10 do begin
writeln(x*i:10:2);
end;
readln;
end.
|
liest x ein
wiederholt die nächste Zeile 10 mal
Ausgabe von x*i auf 10 Stellen und 2 Dezimalen.
wartet auf return-Taste
|
| Befehl |
Kommentar |
readln( variable );
|
Weist das Programm an, vom Benutzer etwas eingeben zu lassen und wartet anschließend auf "return" |
write( 'Hallo Welt!' );
|
Gibt Text auf dem Bildschirm aus. |
writeln( 'Das Ergebnis ist ', x:10:2 );
|
Wie "writeln", nur, dass die nächste Ausgabe am Anfang der nächsten Zeile stattfindet. |
writeln;
|
Geht nur in die nächste Zeile. |
Achtung! Vor jedem "readln" sollte ein "write" stehen, damit der Benutzer weiß, es gibt etwas einzugeben!
program Mul;
uses crt;
var
f1, f2, p: real;
begin
write( '1. Faktor: ' );
readln( f1 );
write( '2. Faktor: ' );
readln( f2 );
p := f1*f2;
writeln( f1:10:2, '*', f2:10:2, '=', p:10:2 );
readln;
end.
Zahlenbeispiel
3x + 4 = 10 | -4
3x = 6 | :3
x = 2
L = { 2 }
Allgemein
ax + b = c | -b
ax = c-b | :a
x = (c-b):a
L = { (c-b):a }
Quelltext
program linear;
uses crt;
var
a, b, c : real;
begin
writeln( 'L”sung der Gleichung a*x + b = c' );
write( 'Gib a (darf nicht 0 sein!) ein: ' );
readln( a );
write( 'Gib b ein: ' );
readln( b );
write( 'Gib c ein: ' );
readln( c );
writeln( 'Das Ergebnis von ',a:4:2,'x + ',b:4:2,' = ',c:4:2,' ist: ' );
writeln( 'L = {',(c-b)/a:10:2,'}' );
readln;
end.
| Rechenart |
Syntax |
Beispiel |
| Addition |
+ |
x:=a+b |
| Subtraktion |
- |
x:=a-b |
| Multiplikation |
* |
x:=a*b |
| Division |
/ div |
x:=a/b; x:= a div b |
| Klammern |
( ) |
x:=(c-b)/a |
| Quadrieren |
sqr |
x:=sqr(a) |
| Radizieren |
sqrt |
x:=sqrt(a) |
Mathematische Zusammenhänge
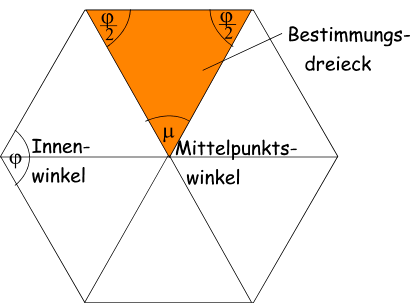
Für ein reguläres n-Eck gilt:
Mittelpunktswinkel: m=360/n
Innenwinkel (siehe Bestimmungsdreieck): j=180-m
Innenwinkelsumme: s = (n-2)*180
Formeln
m = 360/n
j = 180-m
s = (n-2)*180
Berechnungen in PASCAL
program regNEck;
uses crt;
var
n: integer;
m, f, s: real;
begin
writeln( 'Berechnungen am regulaeren n-Eck' );
write( 'Zahl der Ecken :' );
readln( n );
m := 360/n;
f := 180-m;
s := (n-2)*180;
writeln( 'Der Mittelpunktswinkel ist ', m:4:2 );
writeln( 'Der Innenwinkel ist ', f:4:2 );
writeln( 'Die Innenwinkelsumme ist ', s:4:2 );
readln;
end.
Der Anweisungsteil des letzten Beispielprogramms läßt sich in drei Teile zerlegen:
writeln( 'Berechnungen am regulaeren n-Eck' );
write( 'Zahl der Ecken :' );
readln( n );
m := 360/n;
f := 180-m;
s := (n-2)*180;
writeln( 'Der Mittelpunktswinkel ist ', m:4:2 );
writeln( 'Der Innenwinkel ist ', f:4:2 );
writeln( 'Die Innenwinkelsumme ist ', s:4:2 );
Welche Funktion erfüllt der jeweilige Teil?
Die mathematische Datenverarbeitung folgt meistens derm Prinzip "EVA":
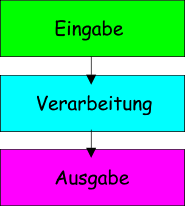
| (E)ingabe |
Das Programm erhält alle zur Berechnung wichtigen Daten; Sie werden in Variablen gespeichert. |
| (V)erarbeitung |
Es werden alle für die Ausgabe notwendigen Berechnungen durchgeführt. |
| (A)usgabe |
Die Ergebnisse der Berechnungen werden an Benutzer ausgegeben. |
Die Erzeugung eines Pascalprogramms folgt dem gleichen Prinzip:
- Eingabe des Quelltextes
- Übersetzung
- Ausgabe des übersetzten Programms


